Robot_bfs

Description

The Robot Moving Institute is using a robot in their local store to transport different items. Of course the robot should spend only the minimum time necessary when travelling from one place in the store to another. The robot can move only along a straight line (track). All tracks form a rectangular grid. Neighbouring tracks are one meter apart. The store is a rectangle N x M meters and it is entirely covered by this grid. The distance of the track closest to the side of the store is exactly one meter. The robot has a circular shape with diameter equal to 1.6 meter. The track goes through the center of the robot. The robot always faces north, south, west or east. The tracks are in the south-north and in the west-east directions. The robot can move only in the direction it faces. The direction in which it faces can be changed at each track crossing. Initially the robot stands at a track crossing. The obstacles in the store are formed from pieces occupying 1m x 1m on the ground. Each obstacle is within a 1 x 1 square formed by the tracks. The movement of the robot is controlled by two commands. These commands are GO and TURN. 
The GO command has one integer parameter n in {1,2,3}. After receiving this command the robot moves n meters in the direction it faces.

The TURN command has one parameter which is either left or right. After receiving this command the robot changes its orientation by 90o in the direction indicated by the parameter.

The execution of each command lasts one second.

Help researchers of RMI to write a program which will determine the minimal time in which the robot can move from a given starting point to a given destination.

Input

The input consists of blocks of lines. The first line of each block contains two integers M <= 50 and N <= 50 separated by one space. In each of the next M lines there are N numbers one or zero separated by one space. One represents obstacles and zero represents empty squares. (The tracks are between the squares.) The block is terminated by a line containing four positive integers B1 B2 E1 E2 each followed by one space and the word indicating the orientation of the robot at the starting point. B1, B2 are the coordinates of the square in the north-west corner of which the robot is placed (starting point). E1, E2 are the coordinates of square to the north-west corner of which the robot should move (destination point). The orientation of the robot when it has reached the destination point is not prescribed. We use (row, column)-type coordinates, i.e. the coordinates of the upper left (the most north-west) square in the store are 0,0 and the lower right (the most south-east) square are M - 1, N - 1. The orientation is given by the words north or west or south or east. The last block contains only one line with N = 0 and M = 0. 

Output

The output contains one line for each block except the last block in the input. The lines are in the order corresponding to the blocks in the input. The line contains minimal number of seconds in which the robot can reach the destination point from the starting point. If there does not exist any path from the starting point to the destination point the line will contain -1. 

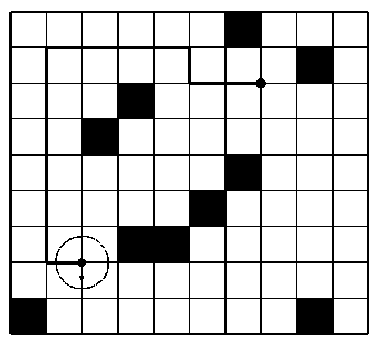
Sample Input

9 10
0 0 0 0 0 0 1 0 0 0
0 0 0 0 0 0 0 0 1 0
0 0 0 1 0 0 0 0 0 0
0 0 1 0 0 0 0 0 0 0
0 0 0 0 0 0 1 0 0 0
0 0 0 0 0 1 0 0 0 0
0 0 0 1 1 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0
1 0 0 0 0 0 0 0 1 0
7 2 2 7 south
0 0

Sample Output

12

【题意】给出一个n*m的图，给出起点和终点的坐标以及刚开始所处的方向，求最少步数，不能走出则输出-1；

【思路】

1、2种命令，一种是向现在所面向的方向走1-3步，另外一种是向左或向右90度转向（不能向后转）。

2、不允许出界和到达障碍物。

3、对搜索进行去重操作的时候需要记录所处位置的方向，因为这个题存在方向的问题，需要注意下，可以设置数组为vis用三维，第三维代表4个方向。

4、存在起点等于终点的情况，还有就是终点是无法到达的。

#include<iostream>
#include<queue>
#include<stdio.h>
#include<string.h>
using namespace std;
const int N=+;
struct node
{
    int x,y;
    int t;
    int pos;
};
node cur;
int n,m,ex,ey,mp[N][N],ans;
bool vis[N][N][];
int dirx[]={-,,,},diry[]={,,,-};
int getPos(char *str)
{
    if(!strcmp(str,"north")) return ;
    if(!strcmp(str,"east")) return ;
    if(!strcmp(str,"south")) return ;
        return ;
}
bool isgo(int x,int y)
{
    if(x<||x>=n||y<||y>=m)
        return false;
    if(mp[x][y]||mp[x+][y]||mp[x][y+]||mp[x+][y+])
        return false ;
    return true;
}
void bfs()
{
    queue<node>qu;
    qu.push(cur);
    vis[cur.x][cur.y][cur.pos]=;
    int ans=-;
    if(cur.x==ex&&cur.y==ey)//起点相同
    {
        printf("0\n");
        return ;
    }
    if(!isgo(ex,ey))//终点出界
    {
        printf("-1\n");
        return ;
    }
    while(!qu.empty())
    {
        node now=qu.front();
        qu.pop();
        int xx=now.x;
        int yy=now.y;
        for(int i=;i<=;i++)
        {
            xx+=dirx[now.pos];
            yy+=diry[now.pos];
            if(!isgo(xx,yy)) break ;
            if(xx==ex&&yy==ey)
            {
                ans=now.t+;
                break;
            }
            if(!vis[xx][yy][now.pos])
            {
                node tmp;
                tmp.x=xx;
                tmp.y=yy;
                tmp.t=now.t+;
                tmp.pos=now.pos;
                vis[xx][yy][tmp.pos]=;
                qu.push(tmp);
            }
        }
        for(int i=;i<;i++)
        {
            if(max(now.pos,i)-min(now.pos,i)==)
                continue;
            if(vis[now.x][now.y][i]) continue;
            node next=now;
            next.t=now.t+;
            next.pos=i;
            vis[next.x][next.y][next.pos]=;
            qu.push(next);
        }
        if(ans!=-) break;
    }
    if(ans!=-) printf("%d\n",ans);
    else printf("-1\n");
    return ;
}
int main()
{
    while(scanf("%d%d",&n,&m))
    {
        if(n==&&m==) break;
        for(int i=;i<=n;i++)
        {
            for(int j=;j<=m;j++)
            {
                scanf("%d",&mp[i][j]);
            }
        }

        memset(vis,,sizeof(vis));
        scanf("%d%d",&cur.x,&cur.y);
        scanf("%d%d",&ex,&ey);
        char op[];
        scanf("%s",op);
        cur.pos=getPos(op);
        cur.t=;
        bfs();

    }
    return ;
}