LSA,pLSA原理及其代码实现
一. LSA
1. LSA原理
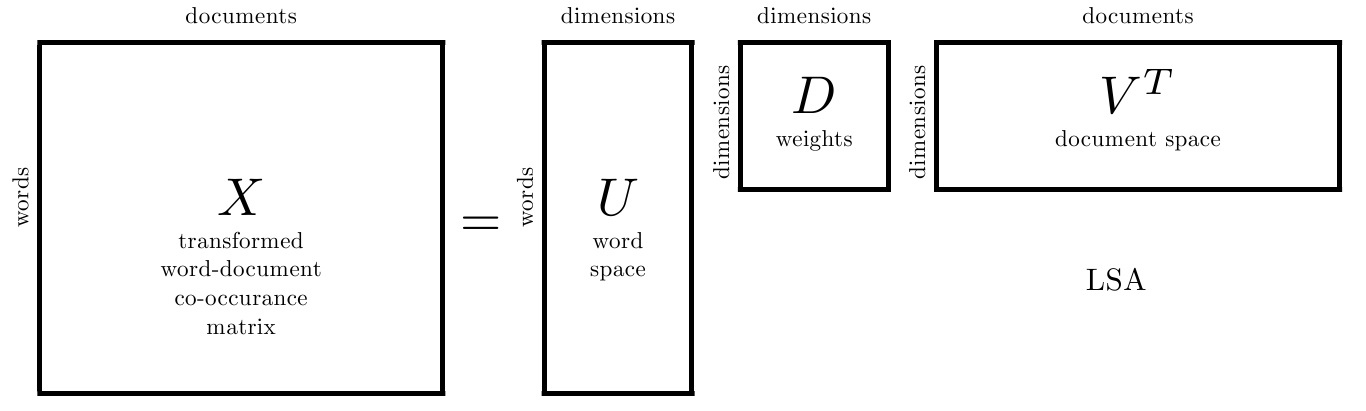
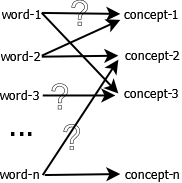
2. LSA的优点
3. LSA的缺点
二. pLSA
pLSA的建模思路分为两种。
1. 第一种思路
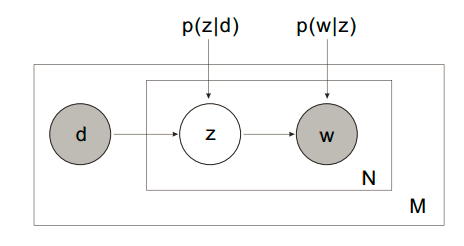
以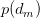 的概率从文档集合
的概率从文档集合 中选择一个文档
中选择一个文档
以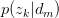 的概率从主题集合
的概率从主题集合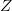 中选择一个主题
中选择一个主题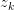
以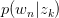 的概率从词集
的概率从词集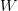 中选择一个词
中选择一个词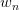
有几点说明:
- 以上变量有两种状态:observed (
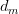 &
&  ) 和 latent (
) 和 latent (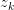 )
)  来自文档,但同时是集合(元素不重复),相当于一个词汇表
来自文档,但同时是集合(元素不重复),相当于一个词汇表
直接的,针对observed variables做建立likelihood function:
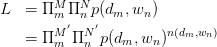
其中,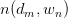 为
为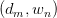 pair出现的次数。为加以区分,之后使用
pair出现的次数。为加以区分,之后使用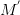 与
与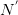 标识对应文档与词汇数量。两边取
标识对应文档与词汇数量。两边取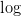 ,得:
,得:
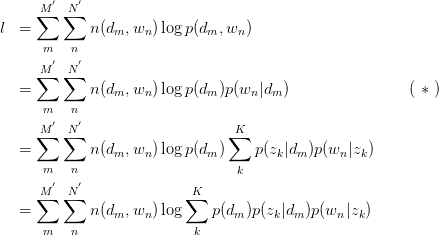
其中,倒数第二步旨在将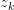 暴露出来。由于likelihood function中
暴露出来。由于likelihood function中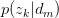 与
与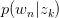 存在latent variable,难以直接使用MLE求解,很自然想到用E-M算法求解。E-M算法主要分为Expectation与Maximization两步。
存在latent variable,难以直接使用MLE求解,很自然想到用E-M算法求解。E-M算法主要分为Expectation与Maximization两步。
假设已知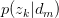 与
与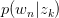 ,求latent variable
,求latent variable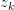 的后验概率
的后验概率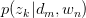
Step 2: Maximization
求关于参数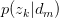 和
和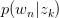 的Complete data对数似然函数期望的极大值,得到最优解。带入E步迭代循环。
的Complete data对数似然函数期望的极大值,得到最优解。带入E步迭代循环。
由 式可得:
式可得:
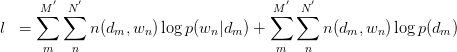
此式后部分为常量。故令:
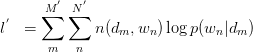
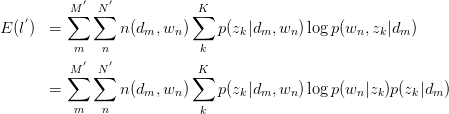
建立以下目标函数与约束条件:
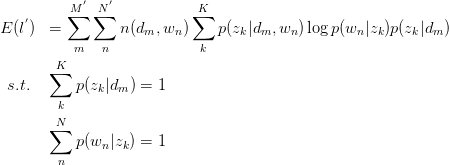
只有等式约束,使用Lagrange乘子法解决:
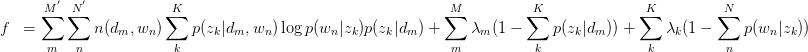
对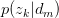 与
与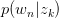 求驻点,得:
求驻点,得:
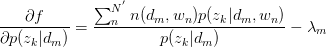
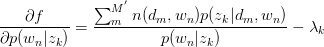
令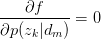 ,得:
,得:
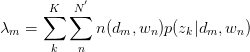 ,故有:
,故有:
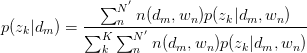
同理,有:
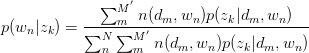
将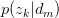 与
与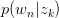 回代Expectation:
回代Expectation:
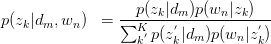 ,循环迭代。
,循环迭代。
pLSA的建模思想较为简单,对于observed variables建立likelihood function,将latent variable暴露出来,并使用E-M算法求解。其中M步的标准做法是引入Lagrange乘子求解后回代到E步。
总结一下使用EM算法求解pLSA的基本实现方法:
2. 第二种思路
这个思路和上面思路的区别就在于对P(d,w)的展开公式使用的不同,思路二使用的是3个概率来展开的,如下:
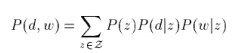
这样子我们后面的EM算法的大致思路都是相同的,就是表达形式变化了,最后得到的EM步骤的更新公式也变化了。当然,思路二得到的是3个参数的更新公式。如下:

你会发现,其实多了一个参数是P(z),参数P(d|z)变化了(之前是P(z|d)),然后P(w|z)是不变的,计算公式也相同。
给定一个文档d,我们可以将其分类到一些主题词类别下。
PLSA算法可以通过训练样本的学习得到三个概率,而对于一个测试样本,其中P(w|z)概率是不变的,但是P(z)和P(d|z)都是需要重新更新的,我们也可以使用上面的EM算法,假如测试样本d的数据,我们可以得到新学习的P(z)和P(d|z)参数。这样我们就可以计算:
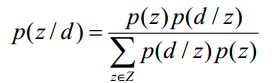
为什么要计算P(z|d)呢?因为给定了一个测试样本d,要判断它是属于那些主题的,我们就需要计算P(z|d),就是给定d,其在主题z下成立的概率是多少,不就是要计算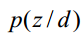 吗。这样我们就可以计算文档d在所有主题下的概率了。
吗。这样我们就可以计算文档d在所有主题下的概率了。
这样既可以把一个测试文档划归到一个主题下,也可以给训练文档打上主题的标记,因为我们也是可以计算训练文档它们的的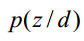 。如果从这个应用思路来说,思路一说似乎更加直接,因为其直接计算出来了
。如果从这个应用思路来说,思路一说似乎更加直接,因为其直接计算出来了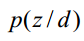 。
。
3. pLSA的优势
4. pLSA的不足
三. pLSA的Python代码实现
#!/usr/bin/env python
# -*- coding: utf-8 -*-
import numpy as np
class Preprocess:
def __init__(self, fname, fsw):
self.fname = fname
# doc info
self.docs = []
self.doc_size = 0
# stop word info
self.sws = []
# word info
self.w2id = {}
self.id2w = {}
self.w_size = 0
# stop word list init
with open(fsw, 'r') as f:
for line in f:
self.sws.append(line.strip())
def __work(self):
with open(self.fname, 'r') as f:
for line in f:
line_strip = line.strip()
self.doc_size += 1
self.docs.append(line_strip)
items = line_strip.split()
for it in items:
if it not in self.sws:
if it not in self.w2id:
self.w2id[it] = self.w_size
self.id2w[self.w_size] = it
self.w_size += 1
self.w_d = np.zeros([self.w_size, self.doc_size], dtype=np.int)
for did, doc in enumerate(self.docs):
ws = doc.split()
for w in ws:
if w in self.w2id:
self.w_d[self.w2id[w]][did] += 1
def get_w_d(self):
self.__work()
return self.w_d
def get_word(self, wid):
return self.id2w[wid]
if __name__ == '__main__':
fname = './data.txt'
fsw = './stopwords.txt'
pp = Preprocess(fname, fsw)
2. plsa.py
#!/usr/bin/env python
# -*- coding: utf-8 -*-
import numpy as np
import time
import logging
def normalize(vec):
s = sum(vec)
for i in range(len(vec)):
vec[i] = vec[i] * 1.0 / s
def llhood(w_d, p_z, p_w_z, p_d_z):
V, D = w_d.shape
ret = 0.0
for w, d in zip(*w_d.nonzero()):
p_d_w = np.sum(p_z * p_w_z[w,:] * p_d_z[d,:])
if p_d_w > 0:
ret += w_d[w][d] * np.log(p_d_w)
return ret
class PLSA:
def __init__(self):
pass
def train(self, w_d, Z, eps):
V, D = w_d.shape
# create prob array, p(d|z), p(w|z), p(z)
p_d_z = np.zeros([D, Z], dtype=np.float)
p_w_z = np.zeros([D, Z], dtype=np.float)
p_z = np.zeros([Z], dtype=np.float)
# initialize
p_d_z = np.random.random([D, Z])
for d_idx in range(D):
normalize(p_d_z[d_idx])
p_w_z = np.random.random([V, Z])
for w_idx in range(V):
normalize(p_w_z[w_idx])
p_z = np.random.random([Z])
normalize(p_z)
# iteration until converge
step = 1
pp_d_z = p_d_z.copy()
pp_w_z = p_w_z.copy()
pp_z = p_z.copy()
while True:
logging.info('[ iteration ] step %d' % step)
step += 1
p_d_z *= 0.0
p_w_z *= 0.0
p_z *= 0.0
# run EM algorithm
for w_idx, d_idx in zip(*w_d.nonzero()):
#print '[ EM ] >>>>>> E step : '
p_z_d_w = pp_z * pp_d_z[d_idx,:] * pp_w_z[w_idx,:]
normalize(p_z_d_w)
#print '[ EM ] >>>>>> M step : '
tt = w_d[w_idx, d_idx] * p_z_d_w
p_w_z[w_idx,:] += tt
p_d_z[d_idx,:] += tt
p_z += tt
normalize(p_w_z)
normalize(p_d_z)
p_z = p_z / w_d.sum()
# check converge
l1 = llhood(w_d, pp_z, pp_w_z, pp_d_z)
l2 = llhood(w_d, p_z, p_w_z, p_d_z)
diff = l2 - l1
logging.info('[ iteration ] l2-l1 %.3f - %.3f = %.3f ' % (l2, l1, diff))
if abs(diff) < eps:
logging.info('[ iteration ] End EM ')
return (l2, p_d_z, p_w_z, p_z)
pp_d_z = p_d_z.copy()
pp_w_z = p_w_z.copy()
pp_z = p_z.copy()
3. main.py
#!/usr/bin/env python
# -*- coding: utf-8 -*-
from preprocess import Preprocess as PP
from plsa import PLSA
import numpy as np
import logging
import time
def main():
# setup logging --------------------------
logging.basicConfig(filename='plsa.log',
level=logging.INFO,
format='%(asctime)s %(filename)s[line:%(lineno)d] %(levelname)s %(message)s',
datefmt='%a, %d %b %Y %H:%M:%S')
#console = logging.StreamHandler()
#console.setLevel(logging.INFO)
#logging.getLogger('').addHandler(console)
# some basic configuration ---------------
fname = './data.txt'
fsw = './stopwords.txt'
eps = 20.0
key_word_size = 10
# preprocess -----------------------------
pp = PP(fname, fsw)
w_d = pp.get_w_d()
V, D = w_d.shape
logging.info('V = %d, D = %d' % (V, D))
# train model and get result -------------
pmodel = PLSA()
for z in range(3, (D+1), 10):
t1 = time.clock()
(l, p_d_z, p_w_z, p_z) = pmodel.train(w_d, z, eps)
t2 = time.clock()
logging.info('z = %d, eps = %f, time = %f' % (z, l, t2-t1))
for itz in range(z):
logging.info('Topic %d' % itz)
data = [(p_w_z[i][itz], i) for i in range(len(p_w_z[:,itz]))]
data.sort(key=lambda tup:tup[0], reverse=True)
for i in range(key_word_size):
logging.info('%s : %.6f ' % (pp.get_word(data[i][1]), data[i][0]))
if __name__ == '__main__':
main()
版权声明:
本文由笨兔勿应所有,发布于http://www.cnblogs.com/bentuwuying。如果转载,请注明出处,在未经作者同意下将本文用于商业用途,将追究其法律责任。
LSA,pLSA原理及其代码实现的更多相关文章
- flume原理及代码实现
转载标明出处:http://www.cnblogs.com/adealjason/p/6240122.html 最近想玩一下流计算,先看了flume的实现原理及源码 源码可以去apache 官网下载 ...
- Java Base64加密、解密原理Java代码
Java Base64加密.解密原理Java代码 转自:http://blog.csdn.net/songylwq/article/details/7578905 Base64是什么: Base64是 ...
- Base64加密解密原理以及代码实现(VC++)
Base64加密解密原理以及代码实现 转自:http://blog.csdn.net/jacky_dai/article/details/4698461 1. Base64使用A--Z,a--z,0- ...
- AC-BM算法原理与代码实现(模式匹配)
AC-BM算法原理与代码实现(模式匹配) AC-BM算法将待匹配的字符串集合转换为一个类似于Aho-Corasick算法的树状有限状态自动机,但构建时不是基于字符串的后缀而是前缀.匹配 时,采取自后向 ...
- Java基础知识强化之集合框架笔记47:Set集合之TreeSet保证元素唯一性和比较器排序的原理及代码实现(比较器排序:Comparator)
1. 比较器排序(定制排序) 前面我们说到的TreeSet的自然排序是根据集合元素的大小,TreeSet将它们以升序排列. 但是如果需要实现定制排序,比如实现降序排序,则要通过比较器排序(定制排序)实 ...
- PHP网站安装程序的原理及代码
原文:PHP网站安装程序的原理及代码 原理: 其实PHP程序的安装原理无非就是将数据库结构和内容导入到相应的数据库中,从这个过程中重新配置连接数据库的参数和文件,为了保证不被别人恶意使用安装文件,当安 ...
- 免费的Lucene 原理与代码分析完整版下载
Lucene是一个基于Java的高效的全文检索库.那么什么是全文检索,为什么需要全文检索?目前人们生活中出现的数据总的来说分为两类:结构化数据和非结构化数据.很容易理解,结构化数据是有固定格式和结构的 ...
- 机器学习之KNN原理与代码实现
KNN原理与代码实现 本文系作者原创,转载请注明出处:https://www.cnblogs.com/further-further-further/p/9670187.html 1. KNN原理 K ...
- 机器学习之AdaBoost原理与代码实现
AdaBoost原理与代码实现 本文系作者原创,转载请注明出处: https://www.cnblogs.com/further-further-further/p/9642899.html 基本思路 ...
随机推荐
- 初步了解yield_python
yield 关键字是在学习python生成器(Generator)时遇到的,对于它及Generator至今我还不能很深入的理解,当前只是把所理解的知识作下记录,以便以后翻查. yield关键字是用来定 ...
- UIWebView和Js交互
在日常的ios项目开发中,我们经常会在原生应用中嵌入web页面,通常我们只是进行一个展示,没有其它的一些功能.但是也有一些项目中需要web页面中的html和native进行交互.但是ios sdk 并 ...
- [poi2010]Hamsters
题意:Tz养了一群仓鼠,他们都有英文小写的名字,现在Tz想用一个字母序列来表示他们的名字,只要他们的名字是字母序列中的一个子串就算,出现多次可以重复计算.现在Tz想好了要出现多少个名字,请你求出最短的 ...
- flashcache
Flashcache系统管理员手册 1.简介Flashcache 是为Linux操作系统开发的块设备回写缓存内核模块,使用了Device Mapper的方式实现,本文档可指导你快速掌握Flashcac ...
- 大数据存储:MongoDB实战指南——常见问题解答
锁粒度与并发性能怎么样? 数据库的读写并发性能与锁的粒度息息相关,不管是读操作还是写操作开始运行时,都会请求相应的锁资源,如果请求不到,操作就会被阻塞.读操作请求的是读锁,能够与其它读操作共享,但是当 ...
- java Map及Map.Entry详解
Map是java中的接口,Map.Entry是Map的一个内部接口. Map提供了一些常用方法,如keySet().entrySet()等方法. keySet()方法返回值是Map中key值的集合:e ...
- AlwaysOn 部分笔记及文档连接
本文主要含有一些AlwaysOn 配置方法及连接. 本想展开详细写一下 无奈隔壁在年会排练节目,那歌唱得我只想赶紧回家!!!!!!!!!!!!!!! http://www.cnblogs.com/d ...
- LUN/PV/VG/LV
存储中的几个概念,参考一些网络资料重新画个图梳理下,如下: LUN:lun是针对存储设备(如磁盘阵列)的逻辑概念,物理上可能就是几块硬盘.那么主机的HBA 卡看到的存储上的存储资源就靠主要两个东西定位 ...
- Linux及文件系统基本介绍
Linux及文件系统基本介绍 1 互联网行业现状 在服务器端市场: 超级计算机 2014年11月的数据显示前500系统中的485个系统都在运行着 Linux 的发布系统,而仅仅只有一台运行着 Wi ...
- HTTP协议解析
1. HTTP版本 HTTP/1.0 HTTP/1.1 HTTP-NG 2. 会话方式 HTTP/1.0 建立连接->请求->响应->断开连接 每次连接只处理一次请求和相应,对资源的 ...
