(小规模)b牌棋盘完美覆盖数

(小规模)b牌棋盘完美覆盖数

考虑一个普通的国际象棋棋盘，它被分成8*8（8行8列）的64个正方形。设有形状一样的多米诺骨牌，每张牌恰好覆盖棋盘上相邻的两个方格（即1*2的骨牌）。那么能否把32个这样的1*2骨牌放到棋盘上，使得任何两张牌均不重叠，每张多米诺骨牌覆盖两个方格，并且棋盘上所有的方格都被覆盖住？我们把这样一种排列称为被多米诺骨牌的完美覆盖。这是一个简单的排列问题，人们能够很快构造许多不同的完美覆盖。但是计算不同的完美覆盖的总数就不是一件容易的事了，不过，这还是有可能做到的。这个数由M.E.Fischer在其一篇名为Statistical Mechanics of Dimers on a Plane Lattice的论文中计算出了不同的完美覆盖总数为： 12988816 = 2⁴ * （901)² 。而后Fischer得出了更一般的公式用来求解1*2骨牌覆盖m*n（m，n至少一个为偶数)方格的公式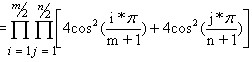，  （符号∏是大写的π，代表连乘）。其实这就是分子生物学著名的二聚物问题。

分析完上面的问题，大家自然会有一个问题，对于一般的1*b的方格来覆盖m*n的棋盘，完美覆盖数又是多少呢？这里，我们称1*b的方格为b-牌(b-omino)。一个已知的事实是，如果一个m*n的棋盘拥有b牌的完美覆盖，那么b是m的一个因子或者b是n的一个因子。本文将给出0<b<5，用来覆盖m*n棋盘的方法数（我们令n不大于m）：

1）b=1 的情况

显然，覆盖方法数只有1种

2）b=2的情况

前面提到了Fischer的三角公式，但是有个问题，如果结果很大的时候，需要给出取模解的时候，用公式就显得力不从心了。

i)而我们发现当n=2的时候，结果数刚好是Fibonacci数列。对于m较大可以用矩阵幂算法解决。

ii)n=3的时候可以推倒出递推式

以及边界条件

其中a_m代表在左上角将第一块骨牌横着放的总方案数，b_m代表在左上角竖着放第一块骨牌的方案数。

不难得出a_m的表达式，继而使用矩阵幂求出大数据求模的解。周源在WC08的讲稿中给出了a_m和b_m的生成函数：

iii) n>3的情况。其实我们注意到b=2，应该能够考虑到二进制，继而考虑到状态压缩动态规划。首先dfs出相邻两行的状态转移方式S_from->S_to,继而用动态规划转移得到每行的方案数H_s。不难看出时间复杂度为O(m*2ⁿ)。菜鱼同学利用特征方程计算了每行的方案数H_s=,由于第二项较小可以忽略，因此H_s约等于0.85*2.414ⁿ，即2ⁿ<Hs<3ⁿ。因此一个更加精确的时间复杂度为O(m*0.85*2.414ⁿ), 不难看出这里n的范围比较小，一般小于12。

3) b=3的情况或者b=4的情况

均可以利用上述推倒递推关系的方法求解。