常州模拟赛d7t3 水管

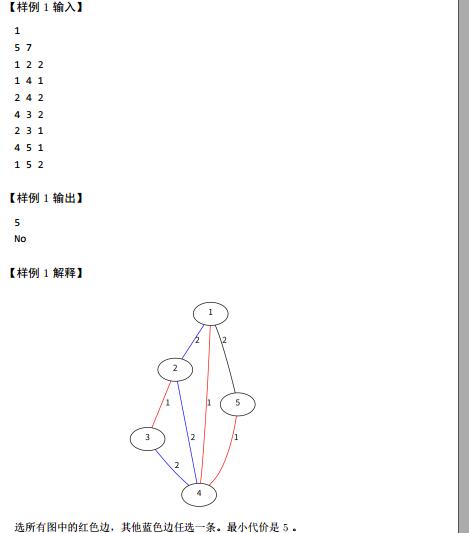
分析：第一问还是很好做的，关键是怎么做第二问.我们可以每次删掉最小生成树上的一条边，然后再求一次最小生成树，看边权和大小和原来的是不是一样的,不过这个做法效率很低.

考虑Kruskal算法的原理，每次加边权最小的边，如果边上的两个点不连通.如果在最小生成树的基础上把不是上面的边给加上去，就会形成环，在环上找除了这条边之外的最大边权，如果等于新加入的这条边，那么就有多个最小生成树.为什么这样呢？我们把最大边拿掉，添加进这条边，两个点还是连通的，边权和一定，只是在Kruskal的时候先考虑了那条最大边而已.

接下来只需要求出若干对点路径上的最大边权就可以了，我们可以用倍增算法来求.

写这道题的时候把w数组写成了e[i].w,挂惨了......以后要对同名数组多留意.

#include <cstdio>
#include <cstring>
#include <iostream>
#include <algorithm>

using namespace std;

const int maxn = ;

int T, n, m, head[maxn], nextt[maxn], to[maxn], w[maxn], tot = ,fa[maxn],d[maxn],f[maxn][],dmax[maxn][];
long long ans;
bool flag = false;

struct node
{
    int u, v, w,use;
}e[maxn];

void add(int x, int y, int z)
{
    w[tot] = z;
    to[tot] = y;
    nextt[tot] = head[x];
    head[x] = tot++;
}

bool cmp(node a, node b)
{
    return a.w < b.w;
}

int find(int x)
{
    if (x == fa[x])
        return x;
    return fa[x] = find(fa[x]);
}

void dfs(int u, int depth,int from)
{
    d[u] = depth;
    f[u][] = from;
    for (int i = head[u]; i; i = nextt[i])
    {
        int v = to[i];
        if (v != from)
        {
            dmax[v][] = w[i];
            dfs(v, depth + , u);
        }
    }
}

int LCA(int x, int y)
{
    if (x == y)
        return ;
    if (d[x] < d[y])
        swap(x, y);
    int maxx = ;
    for (int i = ; i >= ; i--)
        if (d[f[x][i]] >= d[y])
        {
            maxx = max(maxx, dmax[x][i]);
            x = f[x][i];
        }

    if (x == y)
        return maxx;

    for (int i = ; i >= ; i--)
        if (f[x][i] != f[y][i])
        {
            maxx = max(maxx, max(dmax[x][i], dmax[y][i]));
            x = f[x][i];
            y = f[y][i];
        }
    maxx = max(maxx, max(dmax[x][], dmax[y][]));
    return maxx;
}

int main()
{
    scanf("%d", &T);
    while (T--)
    {
        memset(head, , sizeof(head));
        tot = ;
        ans = ;
        flag = false;
        scanf("%d%d", &n, &m);
        memset(d, , sizeof(d));
        memset(f, , sizeof(f));
        memset(dmax, , sizeof(dmax));
        for (int i = ; i <= n; i++)
            fa[i] = i;
        for (int i = ; i <= m; i++)
        {
            int a, b, c;
            scanf("%d%d%d", &a, &b, &c);
            e[i].u = a;
            e[i].v = b;
            e[i].w = c;
            e[i].use = ;
        }
        sort(e + , e +  + m, cmp);
        for (int i = ; i <= m; i++)
        {
            int fx = find(e[i].u), fy = find(e[i].v);
            if (fx != fy)
            {
                add(e[i].u, e[i].v, e[i].w);
                add(e[i].v, e[i].u, e[i].w);
                fa[fx] = fy;
                ans += e[i].w;
                e[i].use = ;
            }
        }
        printf("%lld\n", ans);
        dfs(, ,);
        for (int j = ; j <= ; j++)
            for (int i = ; i <= n; i++)
            {
                f[i][j] = f[f[i][j - ]][j - ];
                dmax[i][j] = max(dmax[i][j - ], dmax[f[i][j - ]][j - ]);
            }
        for (int i = ; i <= m; i++)
            if (!e[i].use && LCA(e[i].u, e[i].v) == e[i].w)
            {
                flag = ;
                break;
            }
        if (flag)
            puts("No");
        else
            puts("Yes");
    }

    return ;
}