python数据处理课程笔记（一）

一、numpy

　　1、numpy中所有元素必须是相同的类型

a=[1,2,3,4,'t']
#列表中有str类型，转换为ndarray时所有元素都转换为str类型
arr1=np.array(a)
print(arr1)
 #输出['1' '2' '3' '4' 't']

　　

　　2、创建：np.array(collection)

　　

　　

#rand只能接收维度参数，不可指定范围，固定范围0～1
arr=np.random.rand(3,4,5)
#randn正态分布

　　

　　3、ndarray的属性：ndim(维度个数)、shape（维度大小）、dtype（数据类型）

　　

　　4、np.zeros():全零；np.ones()：全1 ；np.empty(): 内存里的随机值

　　

　　5、np.arange(start, end ,step): 创建一维数组；np.reshape(): 调整一维数组维度；np.random.shuffle(arr)：打乱数组序列

　　6、转换数组类型：new_arr=old_arr.astype(np.newtype)

　　

　　7、arr*arr是元素相乘，不是矩阵相乘

　　　 列表arr*2会拷贝列表

　　8、索引与切片

　　

　　

　　

　　9、条件索引。多条件组合要用 & | 连接，不能用and、or

　　

　　

　　10、维数转换

import numpy as np
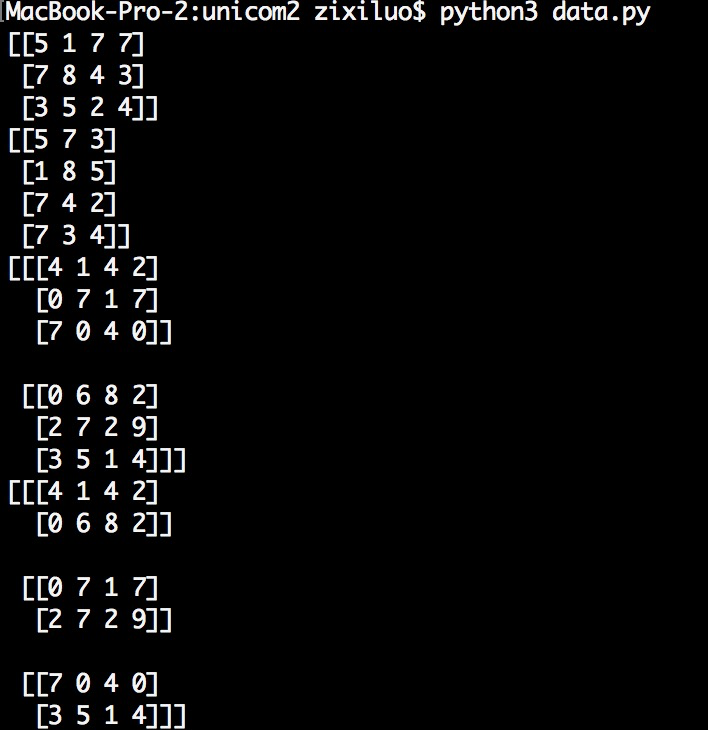
arr=np.random.randint(0,10,(3,4))
print (arr)
arr_t=arr.transpose()#二维直接变成转置矩阵
print(arr_t)
arr3=np.random.randint(0,10,(2,3,4))
print(arr3)
arr3_t=arr3.transpose((1,0,2))#即根据下标改变维度。变为3*2*4
print(arr3_t)

　　

　　11、计算函数

import numpy as np
arr1=np.random.randint(0,10,(3,4))
print(arr1)
print(np.where(arr1>3,1,-1))
print(np.multiply(arr1,arr1))
# 输出
# [[6 7 0 7]
#  [2 9 2 7]
#  [4 0 0 7]]

# [[ 1  1 -1  1]
#  [-1  1 -1  1]
#  [ 1 -1 -1  1]]

# [[36 49  0 49]
#  [ 4 81  4 49]
#  [16  0  0 49]]