BestCoder Round #89 B题---Fxx and game（单调队列）

题目链接

http://acm.hdu.edu.cn/showproblem.php?pid=5945

 

 

问题描述

输入描述

输出描述

输入样例

输出样例

题意：中文题，不再赘述；

思路：  BC题解如下：

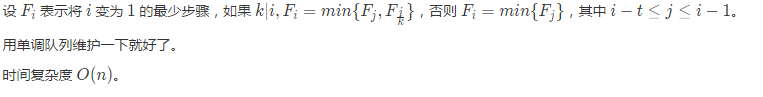
从后往前推，可以得到状态转移方程dp[i]=(dp[k*i],dp[i+l])+1{1<=l<=t}

根据这个转移方程我们需要快速求得min{dp[i+l]}(1<=l<=t)

我们知道这种形式的就是单调队列优化dp的标准形式

维护一个dp[i]从队头到队尾递增的队列 每次算好dp[i]的时候把队尾中dp值大于等于dp[i]的都出队 (出队都是下标比i大的,值又没i优,是无用的)

然后dp[i]=min(dp[a[pre]],dp[k*i])+1

代码如下：

#include <iostream>
#include <algorithm>
#include <stdio.h>
#include <cstring>
#include <cmath>
#include <queue>
#include <set>
#include <bitset>
using namespace std;
typedef long long LL;
int dp[],a[];
int pre,tail;

int main()
{
    int T,x,k,t;
    cin>>T;
    while(T--)
    {
        scanf("%d%d%d",&x,&k,&t);
        pre=,tail=;
        a[tail++]=x;
        dp[x]=;
        for(int i=x-;i>=;i--)
        {
            dp[i] = (t!=)?dp[a[pre]]+:;
            if((1LL*i*k)<=(LL)x) dp[i]=min(dp[i],dp[i*k]+);
            if(a[pre]-t==i) pre++;
            while(dp[a[tail-]]>=dp[i]&&tail>pre) tail--;
            a[tail++]=i;
        }
        printf("%d\n",dp[]);
    }
    return ;
}