清明 DAY 4
~~~~~zhx并没有讲完~~~~~~QAQ~~~~~~










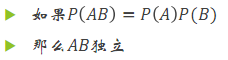

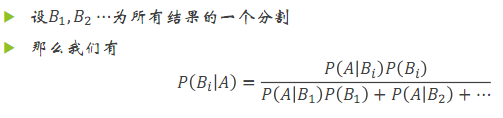

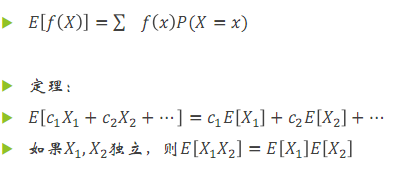
(其实并没有更完)
清明 DAY 4的更多相关文章
- 清明梦超能力者黄YY(idx数组)
清明梦超能力者黄YY https://www.nowcoder.com/acm/contest/206/I 题目描述 黄YY是一个清明梦超能力者,同时也是一个记忆大师.他能够轻松控制自己在梦中的一切, ...
- 清明|TcaplusDB持续为您保驾护航
清明将至,又到一年休闲踏青,祭拜祖先的时机. 清明假期期间,TcaplusDB不停歇,我们将一如既往地守护您的数据,继续做您最坚实的后盾. 在未来,TcaplusDB还将以国产键值型数据库领航者的身 ...
- 清明培训 清北学堂 DAY2
今天是钟皓曦老师的讲授~~ 总结了一下今天的内容: 数论!!! 1.整除性 2.质数 定义: 性质: 3.整数分解定理——算数基本定理 证明: 存在性: 设N是最小不满足唯一分解定理的整数 (1) ...
- 清明培训 清北学堂 DAY1
今天是李昊老师的讲授~~ 总结了一下今天的内容: 1.高精度算法 (1) 高精度加法 思路:模拟竖式运算 注意:进位 优化:压位 程序代码: #include<iostream>#in ...
- 2019清明期间qbxt培训qaq
4.4下午:矩阵qwq part1矩阵乘法: 概念: 一个m×p的矩阵A 乘 一个p×n的矩阵B 得到一个矩阵一个m×n的矩阵AB 其中: 矩阵乘法满足结合律.分配率,不满足交换律 矩阵乘法—solu ...
- 2019清明期间qbxt培训qwq
4.4上午:数学基础 (qwq整成word和cpp了,它居然不能直接把文档附上来) part 1:高精度运算 高精加和高精减就不说了,之前写过博客了qwq,讲一讲高精乘和高精除吧. 1.高精度乘法(不 ...
- 清明 DAY 1
数学基础 Part 1. 高精度计算 Part 2. 模意义下的运算 mod 对一个数取模,其实就是取余数 注意: • 无除法运算 • ...
- 清明 DAY2
数论 数论是研究整数性质的东西 也就是 lim π(x)=x/ ln x (x->无穷) 证明: ∵ p|ab ∴ ab有因子p 设 a=p1k1p2k2......prkr b= ...
- 一个讲课截屏 清明DAY2
灰常混乱 放弃吧........ 不断做平方差公式 到i时,前面已经求出之前数字的逆元了 r是一个比i小的数 第四行×i,r 的逆元 BSGS 暴力枚举枚举到Φ(m)个
- 清明小长假之VUE.JS学习测试码
我们放了四天假,刚好借此机会,系统的了解一下VUE.JS. <!DOCTYPE html> <html> <head> <meta charset=" ...
随机推荐
- IT技术网站博客推荐
CSDN 全球最大中文IT社区,为IT专业技术人员提供最全面的信息传播和服务平台. 51CTO 技术成就梦想 - 中国领先的IT技术网站 itEye Java编程 Spring框架 Ajax技术 ag ...
- 记录一次k8s环境尝试过程(初始方案,现在已经做过很多完善,例如普罗米修斯)
记录一次Team k8s环境搭建过程(初始方案,现在已经做过很多完善,例如普罗米修斯) span::selection, .CodeMirror-line > span > span::s ...
- hadoop工作流程
一)任务流程 1)Mapreduce程序启动一个Jobclient实例,开启整个mapreduce作业 2)Jobclient通过getnewjobld()j接口向Jobtarker发出请求,以获得一 ...
- 时序数据库influxDB存储数据grafana展示数据
一.influxDB简介 InfluxDB是一款用Go语言编写的开源分布式时序.事件和指标数据库,无需外部依赖.该数据库现在主要用于存储涉及大量的时间戳数据,如DevOps监控数据,APP metri ...
- Java 实现《编译原理》简单-语法分析功能-LL(1)文法 - 程序解析
Java 实现<编译原理>简单-语法分析功能-LL(1)文法 - 程序解析 编译原理学习,语法分析程序设计 (一)要求及功能 已知 LL(1) 文法为: G'[E]: E→TE' E'→+ ...
- 背包 || NOIP 2018 D1 T2 || Luogu P5020 货币系统
题面:P5020 货币系统 题解: 显然要求的货币系统是当前货币系统的子集时答案会更优,于是考虑从当前货币系统中删数 一个大数如果能被其他小数表示出来,它就可以去掉 把数据排个序去个重,然后直接背包 ...
- 一个微信小程序跳转到另一个微信小程序
简单来说分两步走: 1.配置项目根目录的 app.json 文件中的 navigateToMiniProgramAppIdList { "pages": [ "pages ...
- java 集合数组排序
//数组排序Integer arr[] = {3,4,2};Arrays.sort(arr);//默认升序Arrays.sort(arr,Comparator.reverseOrder());//传一 ...
- 【2019银川网络赛】L:Continuous Intervals
题目大意:给定一个长度为 N 的序列,定义连续区间 [l, r] 为:序列的一段子区间,满足 [l, r] 中的元素从小到大排序后,任意相邻两项的差值不超过1.求一共有多少个连续区间. 题解:单调栈 ...
- 树形结构根据最后一位的id匹配整个路径
function recursionTreeId(_arr, _id) { _arr.forEach(item => { if (item.id === _id) { optionArr.uns ...
