hdu6333 Problem B. Harvest of Apples（组合数+莫队）

hdu6333 Problem B. Harvest of Apples

题目传送门

题意：

求(0,n)~(m,n)组合数之和

题解：

C(n,m)=C(n-1,m-1)+C(n-1,m)   

设 S(n,m)=C(n,0)+C(n,1)+C(n,2)+。。。+C(n,m)

然后将S(n,m) 通过 第一个公式 拆项

最后化简 变为 S(n,m)=2*S(n-1,m)-C(n-1,m);

即：

所以可以离线用莫队算法

参考博客：链接1、链接2

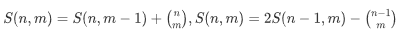
代码：

#include <bits/stdc++.h>
using namespace std;
#define INF 0x3f3f3f3f
typedef long long ll;
const int mod=1e9+;
const int N=1e5+;

/********组合数模板*********/
ll pow_mod(ll a, ll b) {
    ll res = 1ll; a %= mod;
    while(b){
        if(b & ) res = res * a % mod;
        a = a * a % mod;
        b >>= ;
    } return res;
}
ll inv(ll a) { return pow_mod(a, mod-); }
ll F[N], Finv[N];//F是阶乘，Finv是逆元的阶乘
void init() {
    F[] = Finv[] = 1ll;
    for(int i = ; i < N; i ++){
        F[i] = F[i-] * 1ll * (ll)i % mod;
        Finv[i] = Finv[i-] * 1LL * inv(i) % mod;
    }
} // O(n)预处理
ll C(ll n, ll m) {
    if(m <  || m > n) return ;
    return F[n] * 1LL * Finv[n - m] % mod * Finv[m] % mod;
} // O(1)获得组合数C(n,m)
/**************************/

int block[N];
ll res[N];
struct mo
{
    int n,m;
    int id,block;
    bool operator < (const mo &p) const{
      if(block==p.block) return n<p.n;
      else return block<p.block;
    }
}s[N];
int main()
{
    int T;
    scanf("%d",&T);
    int len=sqrt(N+0.5);
    for(int i=;i<T;i++)
    {
        scanf("%d %d",&s[i].n,&s[i].m);
        s[i].block=s[i].m/len;s[i].id=i;
    }
    sort(s,s+T);
    ll ans=;
    init();
    int L=,R=;
    for(int i=;i<T;i++)
    {
        int l=s[i].n,r=s[i].m;
        while(L>l) ans=((ans+C(L-1LL,R))%mod*Finv[])%mod, L--;
        while(L<l) ans=(*ans%mod-C(L,R)+mod)%mod, L++;
        while(R<r) ans=(ans+C(L,R+))%mod, R++;
        while(R>r) ans=(ans-C(L,R)+mod)%mod, R--;
        res[s[i].id]=ans;
    }
    for(int i=;i<T;i++)
        printf("%lld\n",res[i]);
    return ;
}