6411. 【NOIP2019模拟11.06】上网

题目描述

Description

Input

Output

若无解，则输出”Impossible”。

否则第一行输出”Possible”，第二行输出 n 个正整数，依次输出序列 a 中每个数。

Sample Input

5 2 2

2 7

5 3

1 4 2 2 3

4 5 1 4

Sample Output

Possible

6 7 1000000000 6 3

Data Constraint

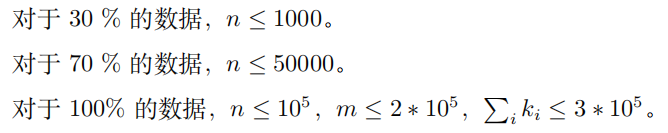
题解

线段树优化连边

ki向xij连边，xi与xi+1间的点向ki连边（线段树），线段树的点从下往上连边

一条从u到v的权值为s的边的意义是f[u]+s<=f[v]，拓扑求max即可

初值就是给出的p和d（不需要求出相对大小然后再搞）

code

#include <algorithm>
#include <iostream>
#include <cstdlib>
#include <cstring>
#include <cstdio>
#define fo(a,b,c) for (a=b; a<=c; a++)
#define fd(a,b,c) for (a=b; a>=c; a--)
#define min(a,b) (a<b?a:b)
#define max(a,b) (a>b?a:b)
using namespace std;
struct type{
	int s,x;
} b[100001];
int a[5000001][3];
int D[1000001];
int ls[1000001];
int d[1000001];
int f[1000001];
int F[1000001];
int c[100002];
int N,n,s,m,i,j,k,l,len,L,R,tot,h,t,mx;
void New(int x,int y,int z)
{
	++len;
	a[len][0]=y;
	a[len][1]=ls[x];
	ls[x]=len;
	a[len][2]=z;
	++D[y];
}
void mt(int t,int l,int r)
{
	int mid=(l+r)/2;
	N=max(N,t+n);
	if (l==r) return;
	mt(t*2,l,mid);
	if (l<mid)
	New(t*2+n,t+n,0);
	else
	New(l,t+n,0);
	mt(t*2+1,mid+1,r);
	if (mid+1<r)
	New(t*2+1+n,t+n,0);
	else
	New(r,t+n,0);
}
void work(int t,int l,int r,int x,int y)
{
	int mid=(l+r)/2;
	if (x<=l && r<=y)
	{
		if (l==r)
		New(l,N,1);
		else
		New(t+n,N,1);
		return;
	}
	if (x<=mid)
	work(t*2,l,mid,x,y);
	if (mid<y)
	work(t*2+1,mid+1,r,x,y);
}
int main()
{
	freopen("web.in","r",stdin);
	freopen("web.out","w",stdout);
	scanf("%d%d%d",&n,&s,&m);
	fo(i,1,n) f[i]=1;
	fo(i,1,s)
	scanf("%d%d",&b[i].x,&b[i].s),f[b[i].x]=b[i].s,F[b[i].x]=b[i].s;
	mt(1,1,n);
	fo(i,1,m)
	{
		++N;
		scanf("%d%d%d",&L,&R,&tot);
		fo(j,1,tot)
		{
			scanf("%d",&c[j]);
			New(N,c[j],0);
		}
		c[0]=L-1;
		c[++tot]=R+1;
		fo(j,1,tot)
		if (c[j-1]+1<=c[j]-1)
		work(1,1,n,c[j-1]+1,c[j]-1);
	}
	h=0;t=0;
	fo(i,1,N)
	if (!D[i])
	d[++t]=i;
	while (h<t)
	{
		for (i=ls[d[++h]]; i; i=a[i][1])
		{
			f[a[i][0]]=max(f[a[i][0]],f[d[h]]+a[i][2]);
			if (F[a[i][0]] && f[a[i][0]]>F[a[i][0]])
			{
				printf("Impossible\n");
				return 0;
			}
			--D[a[i][0]];
			if (!D[a[i][0]])
			d[++t]=a[i][0];
		}
	}
	if (t<N)
	{
		printf("Impossible\n");
		return 0;
	}
	else
	{
		printf("Possible\n");
		fo(i,1,n)
		printf("%d ",f[i]);
		printf("\n");
	}
	fclose(stdin);
	fclose(stdout);
	return 0;
}