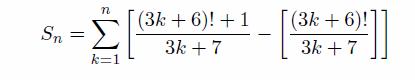威尔逊定理--HDU2973
题目
Problem Description
The math department has been having problems lately. Due to immense amount of unsolicited automated programs which were crawling across their pages, they decided to put Yet-Another-Public-Turing-Test-to-Tell-Computers-and-Humans-Apart on their webpages. In short, to get access to their scientific papers, one have to prove yourself eligible and worthy, i.e. solve a mathematic riddle.
However, the test turned out difficult for some math PhD students and even for some professors. Therefore, the math department wants to write a helper program which solves this task (it is not irrational, as they are going to make money on selling the program).
The task that is presented to anyone visiting the start page of the math department is as follows: given a natural n, compute
where [x] denotes the largest integer not greater than x.
Input
The first line contains the number of queries t (t <= 10^6). Each query consist of one natural number n (1 <= n <= 10^6).
Output
For each n given in the input output the value of Sn.
Sample Input
13
1
2
3
4
5
6
7
8
9
10
100
1000
10000
Sample Output
0
1
1
2
2
2
2
3
3
4
28
207
1609
思路
威尔逊定理及其逆定理、前缀和
威尔逊定理:当且仅当p为素数时:
\]
否则
\]
设
\]
所以当(3k+7)为素数时,a_n为1,否则为0
\]
代码
#include <iostream>
#include <cstring>
#include <cstdio>
#include <cmath>
#include <string>
#include <algorithm>
using namespace std;
typedef long long LL;
const int maxn=1e6+5;
const double pi = acos(-1);
const int mod=1e9+7;
const int N = 1000005;
int vis[N * 4], p[N * 4];
int ans[N];
void Init()\\埃式筛
{
for(int i = 2;(i - 7) / 3 < N;++i)
{
if(!vis[i])
{
if((i - 7) % 3 == 0)
p[(i - 7) / 3] = 1;
for(int j = i + i;j <= N * 4;j += i)
vis[j] = true;
}
}
for(int i = 1;i < N;++i)
ans[i] = ans[i - 1] + p[i];
}
int main()
{
Init();
int T;
cin >> T;
while(T--)
{
int n;
cin >> n;
cout << ans[n] << endl;
}
return 0;
}
[素数定理](https://en.wikipedia.org/wiki/Dirichlet's_theorem_on_arithmetic_progressions)
当a、b为素数时,则形如 a+nb 的素数有无穷多个
威尔逊定理--HDU2973的更多相关文章
- HDU2973(威尔逊定理)
YAPTCHA Time Limit: 10000/5000 MS (Java/Others) Memory Limit: 32768/32768 K (Java/Others) Total S ...
- hdu2973 YAPTCHA【威尔逊定理】
<题目链接> 题目大意: The task that is presented to anyone visiting the start page of the math departme ...
- hdu2973-YAPTCHA-(欧拉筛+威尔逊定理+前缀和)
YAPTCHA Time Limit: 10000/5000 MS (Java/Others) Memory Limit: 32768/32768 K (Java/Others)Total Su ...
- hdu5391 Zball in Tina Town(威尔逊定理)
转载请注明出处: http://www.cnblogs.com/fraud/ ——by fraud Zball in Tina Town Time Limit: 3000/1500 ...
- hdu 2973"YAPTCHA"(威尔逊定理)
传送门 题意: 给出自然数 n,计算出 Sn 的值,其中 [ x ]表示不大于 x 的最大整数. 题解: 根据威尔逊定理,如果 p 为素数,那么 (p-1)! ≡ -1(mod p),即 (p-1)! ...
- HDU 5391 Zball in Tina Town【威尔逊定理】
<题目链接> Zball in Tina Town Problem Description Tina Town is a friendly place. People there care ...
- YAPTCHA UVALive - 4382(换元+威尔逊定理)
题意就是叫你求上述那个公式在不同N下的结果. 思路:很显然的将上述式子换下元另p=3k+7则有 Σ[(p-1)!+1/p-[(p-1)!/p]] 接下来用到一个威尔逊定理,如果p为素数则 ( p -1 ...
- HDU - 2973:YAPTCHA (威尔逊定理)
The math department has been having problems lately. Due to immense amount of unsolicited automated ...
- HDU6608-Fansblog(Miller_Rabbin素数判定,威尔逊定理应用,乘法逆元)
Problem Description Farmer John keeps a website called ‘FansBlog’ .Everyday , there are many people ...
随机推荐
- windows-x64 php5.6+apache2.4+mysql配置
随手一记, 方便以后查找! 1.安装apache2.4 - 下载压缩文件并解压到 D:\Develop\Apache24 - 修改 conf 目录下: httpd.conf 文件 - 服务器目录: ...
- Interceptor for {http://cxf.liuyang.com/}IHiServiceService has thrown exception, unwinding now org.apache.cxf.binding.soap.SoapFault: Error reading XMLStreamReader.
Jquery同域访问:客户端连接服务器访问跨域访问:通过本地html文档,浏览器点击开访问(jquery不支持此访问) 用域名的方式访问http://localhost:8080/CXF_09_jqu ...
- swift - 动态计算文本高度
func heightOfCell(text : String) -> CGFloat { let attributes = [NSFontAttributeName:UI ...
- kali下搭建WiFi钓鱼热点
在linux下建立无线热点并不像在windows下开启网络共享或者使用无线网卡驱动设置AP模式即可. linux下的无线共享要用到两个软件:hostapd(创建无线热点).dnsmasq(dns服务和 ...
- [LeetCode 题解]: Partition List
Given a linked list and a value x, partition it such that all nodes less than x come before nodes gr ...
- Postgresql fillfactor
一个表的填充因子(fillfactor)是一个介于 10 和 100 之间的百分数.100(完全填充)是默认值.如果指定了较小的填充因子,INSERT 操作仅按照填充因子指定的百分率填充表页.每个页上 ...
- web api 跨域问题的解决办法
在APP_Start文件夹下面的WebApiConfig.cs文件夹配置跨域 public static class WebApiConfig { public static void Registe ...
- C#语言各个版本特性(三)
三.查询集合 1.找出List<Product>列表中符合特定条件的所有元素 C#1.1 查询步骤:循环,if判断,打印 product类 using System.Collections ...
- Java NIO Selector选择器
Selector是Java NIO中的一个组件,用于检查一个或多个NIO Channel的状态是否处于可读.可写.如此可以实现单线程管理多个channels,也就是可以管理多个网络链接. 为什么使用S ...
- RabbitMq初探——消息均发
消息均发 前言 由前文 RabbitMq初探——消息分发 可知,rabbitmq自带分发机制——消息会按顺序的投放到该队列下的多个消费者,例如1,3,5投放消费者C1,2,4,6投放消费者C2. 这就 ...