Union Find

并查集

前言

来自知乎，Coursera 上普林斯顿大学的算法公开课，稍微来博客上写写记记。

课程资源：1. Algorithms, Part I 2. Algorithms, Part II 3. Algorithms, 4th Edition

---

Dynamic Connectivity

动态连通性问题，这里的连通是一个等价关系，满足：

1. symmetric: 自反性， p 和 p 自身是连通的。

2. transitive: 传递性，如果 p 和 q 连通，又有 q 和 r 连通，那么 p 和 r 连通。

3. reflexive: 对称性， p 和 q 连通，则 q 和 p 连通。

目标是设计一个高效的数据结构，支持大规模的对象集合，支持频繁的合并和查找操作。

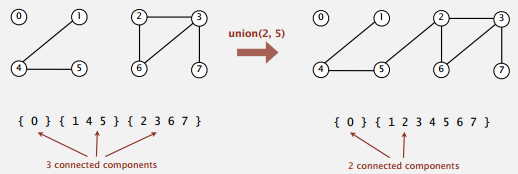
API

Dynamic Connectivity Client

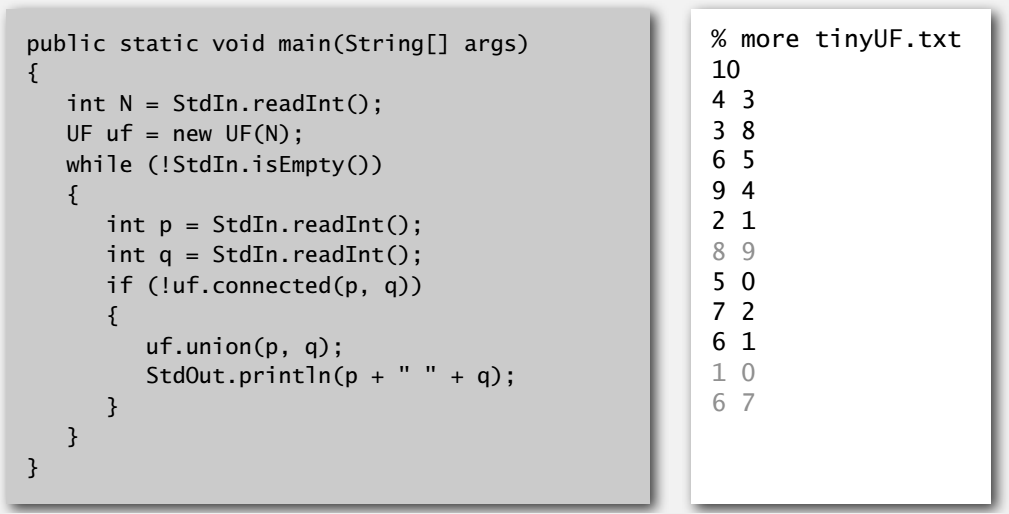
注：想在自己电脑上跑跑的话， algs4.jar ，测试数据在 booksite 上都有。

Quick Find

当且仅当 id[p] 和 id[q] 相等时，p 和 q 才属于同一个连通分量。

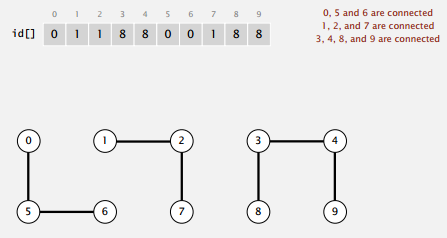
查找操作就只要判断 id 是否相等即可，合并则需要把和 id[p] 相等的所有 id 都改成 id[q] 。

官方示例：QuickFindUF.java。

合并操作

public void union(int p, int q) {
    int pid = id[p];
    int qid = id[q];
    for (int i = 0; i < id.length; i++) {
        if (id[i] == pid) {
            id[i] = qid;
        }
    }
}

其中的 for 循环写成下面这样是错的。

for (int i = 0; i < id.length; i++) {
    if (id[i] == id[p]) {
        id[i] = id[q];
    }
}

id[p] 在循环中变成了 id[q] ，原来相等的关系变成不等，导致数组中排在其后面的本应改变的对象无法更新 id 。举例来说，上面那张图要是这样合并 5 和 9 的话， 6 与 7 的 id 就还会是 1 ， 而不会更新成 8 。

这种实现，查找操作很快，但对 n 个对象进行 n 次合并需要访问数组 n^2 次，平方级别对大规模的数据来说是不可接受的。

Quick Union

将连通分量抽象成树， id[p] 表示 p 的父节点。

查找操作要检查 p q 是否有相同的根节点，合并操作则只要把 p 根节点的父节点改成 q 的根节点即可，只改变了 id[] 中的一个值。

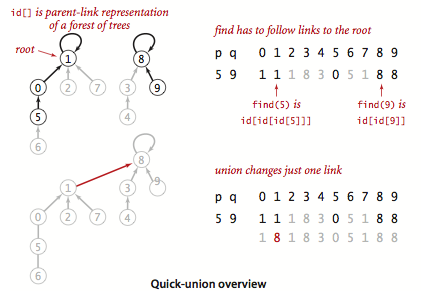
官方示例：QuickUnionUF.java。

找根节点

private int root(int i) {
    while (i != id[i]) {
        i = id[i];
    }

    return i;
}

这样查找和合并的实现都可以写得和简洁，就上面的 while() 需要考虑下。

因为树有可能很高，找根节点就需要访问很多次数组，查找和合并操作都不快。

Improvements

在 quick union 基础上加以改进。

Weighted Quick Union

合并时加以一定约束：保证是将小树合并到大树上，来避免出现过高的树。

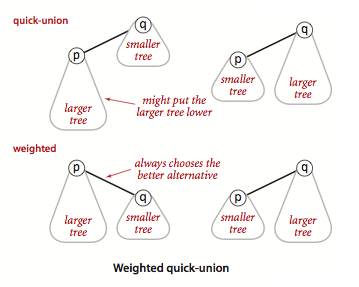
这样一来任意的节点 x 的深度最多为 lgN （以 2 为底），N 为 100 w 时深度最多是 20， 10 亿时是 30 ，相对来说可以支持较大规模的数据了。

至于为什么是 lgN ，可以粗略的这么想：节点 x 的深度只有在其所在的树 T1 被合并到另一个更大的树 T2 时才会加一，而 size(T2) >= size(T1)，那么节点 x 所在的树的大小至少会变成两倍。而总共 N 个节点，最多可以两倍 lgN 次，深度加一 lgN 次，即深度最多为 lgN 。

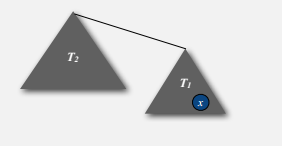
官方示例：WeightedQuickUnionUF.java。

合并

public void union(int p, int q) {
    int i = root(p);
    int j = root(q);
    if (i == j) {
        return;
    }
    if (sz[i] < sz[j]) {
        id[i] = j;
        sz[j] += sz[i];
    }
    else {
        id[j] = i;
        sz[i] += sz[j];
    }
}

Path Compression

此外还可以加上路径压缩，来进一步改善性能。所谓路径压缩，就是在找到根节点之后，把经过的点都直接连到根节点上，降低树高。

举例来说，下面合并 5 和 9 。

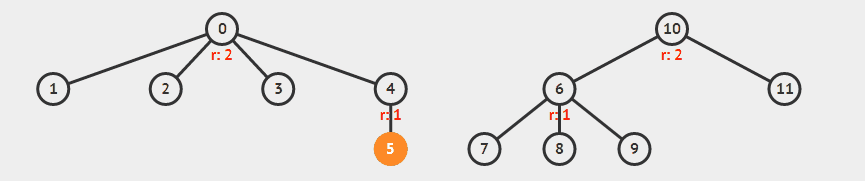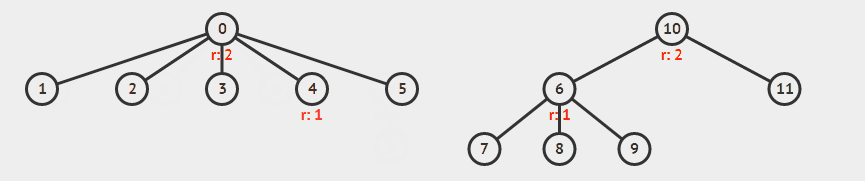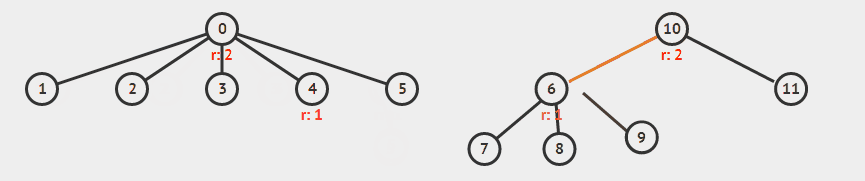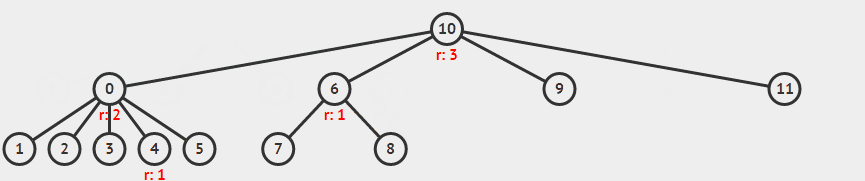
录自 visualgo 。

官方示例：WeightedQuickUnionPathCompressionUF.java。

路径压缩

 public int root(int p) {
    int root = p;
    while (root != id[root])
        root = id[root];
    while (p != root) {
        int newp = id[p];
        id[p] = root;
        p = newp;
    }
    return root;
}

详细的性能分析比较复杂，反正就是很快啦。

Applications

并查集有很多应用，上面的动态连接问题就算，视频里还有个物理系统方面的渗透（percolation）问题的例子。

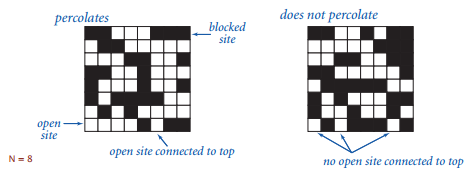
黑色表示方块是闭合的，如果上下存在连通的白色路径，则认为这个系统是可以渗透的。这是一个抽象的模型，实际上比如说可以是一块材料，白色表示可导电，那么系统渗透的话，整块材料就可以导电之类的。

其中方块是白色的概率为 p ，当 N 很大的时候，存在一个阈值 p* ，若 p >= p* 则几乎可以确定系统是可以渗透的。但这样的阈值函数图像很陡峭，问题就是如何求出这个阈值。

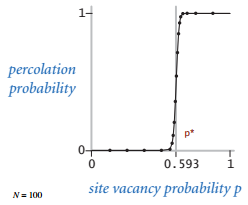
Monte Carlo Simulation

这个问题，蒙特卡罗模拟可以解决。该方法随机地把黑色方块变成白色，直到系统可以渗透，然后用白色方块所占的比例来近似 p* 。举例来说， 下面近似的 p* = 204/400 = 5.1 。

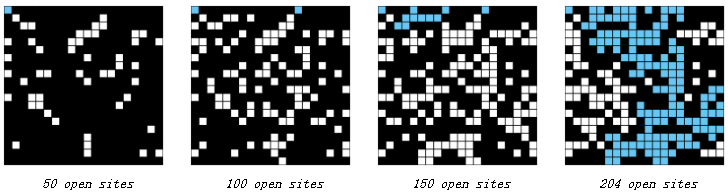
再重复做多次这样的模拟，就能得到比较精确的阈值 p* 。其实第一个编程作业就是渗透问题，里面是多次模拟后再求均值求方差，最后用概率论的知识算了 p* 置信度为 95% 的取值区间。。。

并查集是用在判断系统是否渗透上的。我们用 0 到 N^2 - 1 给每个方块编号，把相邻（上下左右）的白色方块合并起来，要是一个连通分量里同时含有第一行和最后一行的方块，那么系统就是可以渗透的。一个个检查第一行和最后一行的方块有点麻烦，我们可以假装上下各有一个方块，上面的和第一行全部方块都相连，下面类似。那么我们只要判断这两个虚拟方块是否连通即可，连通则系统可以渗透。

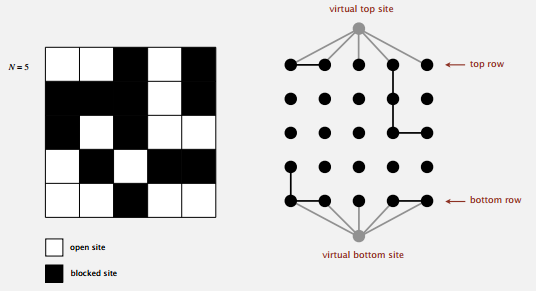
这样在随机打开方块之后，要把它和相邻的白色方块（如果有的话）连接起来，再判断那两个虚拟方块是否连通，如果不连通则继续随机打开直到它们连通，连通则系统可以渗透，就可以用白方块个数除 N^2 得到近似的阈值啦。

最后，因为这其实就是第一次编程作业的题目，我具体的实现等到下次再说。