图的最短路径---弗洛伊德(Floyd)算法浅析

算法介绍

和Dijkstra算法一样，Floyd算法也是为了解决寻找给定的加权图中顶点间最短路径的算法。不同的是，Floyd可以用来解决“多源最短路径”的问题。

算法思路

算法需要引入两个二维数组ShortPathTable和Patharc。ShortPathTable表示顶点到顶点的最短路径权值和的矩阵，Patharc表示对应顶点的最小路径的前驱矩阵。在为分析任何顶点之前，ShortPathTable初始化为图的邻接矩阵。

假设图G有N个顶点，那么需要对矩阵ShortPathTable进行N次更新。

第一次更新时如果:

ShortPathTable[v][w] > ShortPathTable[v][0]+ShortPathTable[0][w]
//(ShortPathTable[v][0]+ShortPathTable[0][w]表示"v与w之间经过第1个顶点的距离")

则更新:

ShortPathTable[v][w]为ShortPathTable[v][0]+ShortPathTable[0][w]

同时因为有变化，所以Patharc矩阵对应的Patharc[v][w]和Patharc[w][v]修改为当前中转的顶点的下标0。

同理，第k次更新时:如果"ShortPathTable[v][w]的距离" > “ShortPathTable[v][k]+ShortPathTable[k][w]”，则更新ShortPathTable[v][w]为"ShortPathTable[v][k]+a[k][w]"。

循环更新N次后操作完成。

算法示例

初始化时该网图矩阵(ShortPathTable)如下：

[015∞∞∞∞∞∞10375∞∞∞∞530∞17∞∞∞∞7∞02∞3∞∞∞5120369∞∞∞7∞30∞5∞∞∞∞36∞027∞∞∞∞95204∞∞∞∞∞∞740]
\left[
\begin{matrix}
0 & 1 & 5 & ∞ & ∞ & ∞ & ∞ & ∞ & ∞ \\
1 & 0 & 3 & 7 & 5 & ∞ & ∞ & ∞ & ∞ \\
5 & 3 & 0 & ∞ & 1 & 7 & ∞ & ∞ & ∞\\
∞ & 7 & ∞ & 0 & 2 & ∞ & 3 & ∞ & ∞\\
∞ & 5 & 1 & 2 & 0 & 3 & 6 & 9 & ∞\\
∞ & ∞ & 7 & ∞ & 3 & 0 & ∞ & 5 & ∞\\
∞ & ∞ & ∞ & 3 & 6 & ∞ & 0 & 2 & 7\\
∞ & ∞ & ∞ & ∞ & 9 & 5 & 2 & 0 & 4\\
∞ & ∞ & ∞ & ∞ & ∞ & ∞ & 7 & 4 & 0\\
\end{matrix}
\right]
⎣⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎡​015∞∞∞∞∞∞​10375∞∞∞∞​530∞17∞∞∞​∞7∞02∞3∞∞​∞5120369∞​∞∞7∞30∞5∞​∞∞∞36∞027​∞∞∞∞95204​∞∞∞∞∞∞740​⎦⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎤​

Patharc初始化为：

[012345678012345678012345678012345678012345678012345678012345678012345678012345678]
\left[
\begin{matrix}
0 & 1 & 2 & 3 & 4 & 5 & 6 & 7 & 8 \\
0 & 1 & 2 & 3 & 4 & 5 & 6 & 7 & 8 \\
0 & 1 & 2 & 3 & 4 & 5 & 6 & 7 & 8 \\
0 & 1 & 2 & 3 & 4 & 5 & 6 & 7 & 8 \\
0 & 1 & 2 & 3 & 4 & 5 & 6 & 7 & 8 \\
0 & 1 & 2 & 3 & 4 & 5 & 6 & 7 & 8 \\
0 & 1 & 2 & 3 & 4 & 5 & 6 & 7 & 8 \\
0 & 1 & 2 & 3 & 4 & 5 & 6 & 7 & 8 \\
0 & 1 & 2 & 3 & 4 & 5 & 6 & 7 & 8 \\
\end{matrix}
\right]
⎣⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎡​000000000​111111111​222222222​333333333​444444444​555555555​666666666​777777777​888888888​⎦⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎤​

程序循环第一次，即k=0时，也就是所有顶点都经过v0v_0v0​中转时，没有变化。

当k=1时，也就是说所有顶点都经过v1v_1v1​中转，此时，当v=0时，原本ShortPathTable[0][2]=5，现在由于ShortPathTable[0][1]+ShortPathTable[1][2]=4。所以使ShortPathTable[0][2]=4，同理ShortPathTable[0][３]＝８，ShortPathTable[0][4]=6．当v=2, 3, 4时也修改了数据。同时在矩阵Patharc上也需要做操作。

此时ShortPathTable：

[01486∞∞∞∞10375∞∞∞∞4301017∞∞∞871002∞3∞∞65120369∞∞∞7∞30∞5∞∞∞∞36∞027∞∞∞∞95204∞∞∞∞∞∞740]
\left[
\begin{matrix}
0 & 1 & 4 & 8 & 6 & ∞ & ∞ & ∞ & ∞ \\
1 & 0 & 3 & 7 & 5 & ∞ & ∞ & ∞ & ∞ \\
4 & 3 & 0 & 10 & 1 & 7 & ∞ & ∞ & ∞\\
8 & 7 & 10 & 0 & 2 & ∞ & 3 & ∞ & ∞\\
6 & 5 & 1 & 2 & 0 & 3 & 6 & 9 & ∞\\
∞ & ∞ & 7 & ∞ & 3 & 0 & ∞ & 5 & ∞\\
∞ & ∞ & ∞ & 3 & 6 & ∞ & 0 & 2 & 7\\
∞ & ∞ & ∞ & ∞ & 9 & 5 & 2 & 0 & 4\\
∞ & ∞ & ∞ & ∞ & ∞ & ∞ & 7 & 4 & 0\\
\end{matrix}
\right]
⎣⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎡​01486∞∞∞∞​10375∞∞∞∞​4301017∞∞∞​871002∞3∞∞​65120369∞​∞∞7∞30∞5∞​∞∞∞36∞027​∞∞∞∞95204​∞∞∞∞∞∞740​⎦⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎤​

此时的Patharc：

[011115678012345678112145678111345678112345678012345678012345678012345678012345678]
\left[
\begin{matrix}
0 & 1 & 1 & 1 & 1 & 5 & 6 & 7 & 8 \\
0 & 1 & 2 & 3 & 4 & 5 & 6 & 7 & 8 \\
1 & 1 & 2 & 1 & 4 & 5 & 6 & 7 & 8 \\
1 & 1 & 1 & 3 & 4 & 5 & 6 & 7 & 8 \\
1 & 1 & 2 & 3 & 4 & 5 & 6 & 7 & 8 \\
0 & 1 & 2 & 3 & 4 & 5 & 6 & 7 & 8 \\
0 & 1 & 2 & 3 & 4 & 5 & 6 & 7 & 8 \\
0 & 1 & 2 & 3 & 4 & 5 & 6 & 7 & 8 \\
0 & 1 & 2 & 3 & 4 & 5 & 6 & 7 & 8 \\
\end{matrix}
\right]
⎣⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎡​001110000​111111111​122122222​131333333​144444444​555555555​666666666​777777777​888888888​⎦⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎤​

接下来就是k=2，一直到k=8，表示针对每个顶点做中转得到的计算结果。

(最终形成的ShortPathTable和Patharc矩阵我就不画了…用markdown来画矩阵好麻烦…)

代码说明

基本定义

	private final int INFINITY = 65535;
	public int MAXVEX;
	public int[][] Patharc;
	public int[][] ShortPathTable;
	//这里直接使用上图的邻接矩阵了，避免了图转矩阵的步骤
	public int[][] maze = {
            {0, 1, 5, INFINITY, INFINITY, INFINITY, INFINITY, INFINITY, INFINITY },
            {1, 0, 3, 7, 5, INFINITY, INFINITY, INFINITY, INFINITY },
            {5, 3, 0, INFINITY, 1, 7, INFINITY, INFINITY, INFINITY },
            {INFINITY, 7, INFINITY, 0, 2, INFINITY, 3, INFINITY, INFINITY },
            {INFINITY, 5, 1, 2, 0, 3, 6, 9, INFINITY},
            {INFINITY, INFINITY, 7, INFINITY, 3, 0, INFINITY, 5, INFINITY},
            {INFINITY, INFINITY, INFINITY, 3, 6, INFINITY, 0, 2, 7},
            {INFINITY, INFINITY,INFINITY, INFINITY, 9, 5, 2, 0, 4},
            {INFINITY, INFINITY, INFINITY, INFINITY, INFINITY, INFINITY, 7, 4,0}
        };

实现代码

	public Floyd() {
		this.MAXVEX = maze.length;
		ShortPathTable = maze;
		Patharc = new int[MAXVEX][MAXVEX];
	}

	public void ShortestPath_Floyd() {
		int v, w, k;
		for (v = 0; v < MAXVEX; v++) {
			for (w = 0; w < MAXVEX; w++) {
				Patharc[v][w] = w;
			}
		}

		//核心代码
		for (k = 0; k < MAXVEX; k++) {
			for (v = 0; v < MAXVEX; v++) {
				for (w = 0; w < MAXVEX; w++) {
					if(ShortPathTable[v][w] > (ShortPathTable[v][k] + ShortPathTable[k][w])) {
						ShortPathTable[v][w] = ShortPathTable[v][k] + ShortPathTable[k][w];
						Patharc[v][w] = Patharc[v][k];
					}
				}
			}
		}

		/**
		 * 最短路径的显示
		 */
		for (v = 0; v < MAXVEX; v++) {
			for (w = 0; w < MAXVEX; w++) {
				System.out.print(v + "-" + "-" + w + " weight:" + ShortPathTable[v][w] + " ");
				k = Patharc[v][w];
				System.out.print("path: " + v);
				while(k != w) {
					System.out.print("->" + k);
					k = Patharc[k][w];
				}
				System.out.print("->" + w + "\n");
			}
			System.out.println();
		}

	}

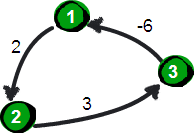
注意：弗洛伊德(Floyd)算法不能解决带有"负权回路"(又称负权环)。因为带有“负权回路”的图没有最短路。例如下面这个图就不存在1号顶点到3号顶点的最短路径。因为1->2->3->1->2->3->…->1->2->3这样路径中，每绕一次1->-2>3这样的环，最短路就会减少1，永远找不到最短路。其实如果一个图中带有“负权回路”那么这个图则没有最短路。