Codeforces 1009D：Relatively Prime Graph

D. Relatively Prime Graph

time limit per test

2 seconds

memory limit per test

256 megabytes

input

standard input

output

standard output

Let's call an undirected graph G=(V,E)G=(V,E) relatively prime if and only if for each edge (v,u)∈E(v,u)∈E  GCD(v,u)=1GCD(v,u)=1 (the greatest common divisor of vv and uu is 11). If there is no edge between some pair of vertices vv and uu then the value of GCD(v,u)GCD(v,u) doesn't matter. The vertices are numbered from 11 to |V||V|.

Construct a relatively prime graph with nn vertices and mm edges such that it is connected and it contains neither self-loops nor multiple edges.

If there exists no valid graph with the given number of vertices and edges then output "Impossible".

If there are multiple answers then print any of them.

Input

The only line contains two integers nn and mm (1≤n,m≤1051≤n,m≤105) — the number of vertices and the number of edges.

Output

If there exists no valid graph with the given number of vertices and edges then output "Impossible".

Otherwise print the answer in the following format:

The first line should contain the word "Possible".

The ii-th of the next mm lines should contain the ii-th edge (vi,ui)(vi,ui) of the resulting graph (1≤vi,ui≤n,vi≠ui1≤vi,ui≤n,vi≠ui). For each pair (v,u)(v,u)there can be no more pairs (v,u)(v,u) or (u,v)(u,v). The vertices are numbered from 11 to nn.

If there are multiple answers then print any of them.

Examples

input

Copy

5 6

output

Copy

Possible
2 5
3 2
5 1
3 4
4 1
5 4

input

Copy

6 12

output

Copy

Impossible

Note

Here is the representation of the graph from the first example: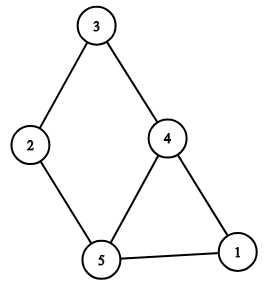

题意：有n个点，编号为1~n。有m条边，要求每条边的顶点的最大公约数为1（并且没有平行边和环），如果这些点和边能组成无向的连通图，并且边和顶点都没有剩余，则输出Possible，并输出可能的边（用顶点表示），否则输出Impossible

AC代码：

#include <stdio.h>
#include <string.h>
#include <iostream>
#include <algorithm>
#include <math.h>
#include <limits.h>
#include <map>
#include <stack>
#include <queue>
#include <vector>
#define ll long long
#define ms(a) memset(a,0,sizeof(a))
#define pi acos(-1.0)
#define INF 0x3f3f3f3f
const double E=exp(1);
const int maxn=1e6+10;
using namespace std;
ll gcd(ll a,ll b)
{
	return b==0?a:gcd(b,a%b);
}
ll vis[maxn][2];
int main(int argc, char const *argv[])
{
	ios::sync_with_stdio(false);
	ll n,m;
	cin>>n>>m;
	ms(vis);
	if(m<n-1)//只有两个点，一条边
		cout<<"Impossible"<<endl;
	else
	{
		ll k=0;
		for(ll i=1;i<n;i++)
			for(ll j=i+1;j<=n;j++)
			{
				if(gcd(i,j)==1)//i和j的最大公约数为1，说明两点可以相连
				{
					vis[k][0]=i;
					vis[k][1]=j;
					k++;//i，j看做边的两点，并更新k的值
					if(k>m)
						break;//这个停止不能少！！！要不然数太多，数组存不下！！
				}
			}
		if(k<m)
			cout<<"Impossible"<<endl;
		else
		{
			cout<<"Possible"<<endl;
			for(int i=0;i<m;i++)
			{
				cout<<vis[i][0]<<" "<<vis[i][1]<<endl;
			}
		}
	}
	return 0;
}