K-mean和k-mean++

(1)k-mean聚类

k-mean聚类比较容易理解就是一个计算距离，找中心点，计算距离，找中心点反复迭代的过程，

给定样本集D={x₁,x₂,...,x_m},k均值算法针对聚类所得簇划分C={C₁,C₂,...,C_k}最小化平方误差

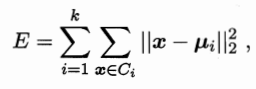
μi表示簇Ci的均值向量，在一定程度上刻画了簇内样本围绕均值向量的紧密程度，E值越小则簇内样本相似度越高。

下边是k均值算法的具体实现的算法

k均值算法的缺点是：(1)对于离群点和孤立点敏感；(2)k值选择; (3)初始聚类中心的选择； (4)只能发现球状簇。

k均值问题用于分布式的环境下：

分布式环境下肯定是在一块一块的计算的，如果在每个块中都加入选择的k个点，则在每个块中都进行简单的聚类。之后，，，，，

（2）k-mean++

k-mean算法有各种缺陷问题，比如上边的缺点（3）初始聚类中心的选择，选择不同的初始聚类中心点可能得到不同的结果，虽然可以多次选择不同的初始点，多次计算，但是这样无意中增加了更多的计算量，因此提出了k-mean++算法，k-mean++算法主要是针对初始时选择聚类中心的问题，

k-means++算法选择初始seeds的基本思想就是：初始的聚类中心之间的相互距离要尽可能的远。wiki上对该算法的描述是如下:

1. 从输入的数据点集合中随机选择一个点作为第一个聚类中心
2. 对于数据集中的每一个点x，计算它与最近聚类中心(指已选择的聚类中心)的距离D(x)
3. 选择一个新的数据点作为新的聚类中心，选择的原则是：D(x)较大的点，被选取作为聚类中心的概率较大
4. 重复2和3直到k个聚类中心被选出来
5. 利用这k个初始的聚类中心来运行标准的k-means算法

从上面的算法描述上可以看到，算法的关键是第3步，如何将D(x)反映到点被选择的概率上，一种算法如下(详见此地)：

1. 先从我们的数据库随机挑个随机点当“种子点”
2. 对于每个点，我们都计算其和最近的一个“种子点”的距离D(x)并保存在一个数组里，然后把这些距离加起来得到Sum(D(x))。
3. 然后，再取一个随机值，用权重的方式来取计算下一个“种子点”。这个算法的实现是，先取一个能落在Sum(D(x))中的随机值Random，然后用Random -= D(x)，直到其<=0，此时的点就是下一个“种子点”。
4. 重复2和3直到k个聚类中心被选出来
5. 利用这k个初始的聚类中心来运行标准的k-means算法

可以看到算法的第三步选取新中心的方法，这样就能保证距离D(x)较大的点，会被选出来作为聚类中心了。至于为什么原因很简单，如下图 所示：

假设A、B、C、D的D(x)如上图所示，当算法取值Sum(D(x))*random时，该值会以较大的概率落入D(x)较大的区间内，所以对应的点会以较大的概率被选中作为新的聚类中心。So it's work!

更过关于k-mean++的实现可以参见 http://blog.chinaunix.net/uid-24774106-id-3412491.html

duiyuk-mean算法的每个缺点的改进算法 http://blog.csdn.net/u010536377/article/details/50884416