小白初识 - 快速排序（QuickSort）

我个人觉得快速排序和归并排序有相似之处，都是用到了分治的思想，将大问题拆分成若干个小问题。

不同的地方是归并排序是先把大问题拆分好了之后再排序，而快速排序则是一边拆分，一边排序。

快速排序的原理就是，针对一个数组，我们任意选取数组中的一个数，将数组中的数与它一一比较，如果小于它呢，就放左边，

大于它呢，就放右边。再针对左边和右边的重复上述动作即可，所以也要用到递归。

先来看看递归公式：quickSort(p...r) = quickSort(p...q-1) + quickSort(q+1, r)，我们一般选数组末尾的数作为用来比较的数。

再来看看对于一个数组的快速排序演示图：

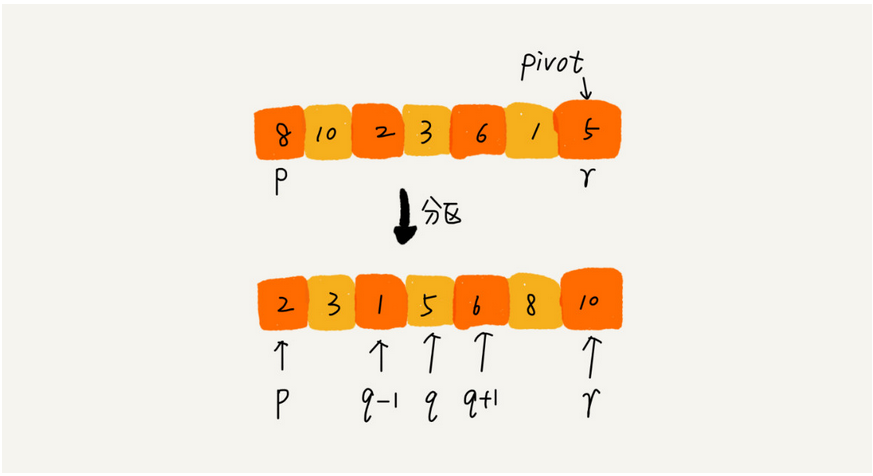
以下是我的Java代码实现：

 package com.structure.sort;

 /**
  * @author zhangxingrui
  * @create 2019-01-27 22:52
  **/
 public class QuickSort {

     public static void main(String[] args) {
         int[] numbers = {9, 1, 2, 8, 7, 3, 6, 4, 3, 5, 0, 9, 19, 39, 25, 34, 17, 24, 23, 34, 20};
 //        int[] numbers = {3,1,2};
         // 快速排序借助递归来实现，重要的是要找到递归的终结条件（不然容易发生堆栈异常）
         // 递推公式：quickSort(p...r) = merge(p, q - 1) + merge(q+1, r)
         // 终结条件：p >= r
         quickSort(numbers, 0, numbers.length - 1);
         for (int number : numbers) {
             System.out.println(number);
         }
     }

     private static void quickSort(int[] numbers, int p, int r){
         if(p >= r)
             return;
         int q = partition(numbers, p, r);
         quickSort(numbers, p, q - 1);
         quickSort(numbers, q + 1, r);
     }

     /**
      * @Author: xingrui
      * @Description: 分区
      * @Date: 23:13 2019/1/27
      */
     private static int partition(int[] numbers, int p, int r){
         int k = numbers[r];
         int i = p;

         for (int j = p; j <= r; ++j) {
             if(numbers[j] < k){
                 int temp = numbers[i];
                 numbers[i] = numbers[j];
                 numbers[j] = temp;
                 i++;
             }
         }
         numbers[r] = numbers[i];
         numbers[i] = k;
         return i;
     }

 }

其中的重点就是分区的函数是如何实现的，分区这里实现用的其实是类似选择排序的方式，将指定位置的两个元素进行交换，

从而实现k的左边都是小于k的，k的右边都是大于k的。

最后我们来问三个问题：

1.快速排序是稳定的排序算法吗？

2.快速排序是原地排序吗？

3.快速排序的时间复杂度是多少？

解答：

1.快速排序不是稳定的排序算法，比如我们现在有一个数组[4, 10, 9, 8, 10, 7, 8]，根据分区部分代码的交换逻，第一个十会被交换到

第二个十的后边儿，所以快排不是稳定的排序算法。

2.快排是原地排序。整个排序过程中没有申请多余的内存空间。

3.快速排序的时间复杂度计算比较复杂，主要考虑两种情况：

当每次分区都差不多可以从中间分区，那么快排的时间复杂度计算方式与归并排序的时间复杂度计算方式相仿，都是O(nlogn)；

当每次分区都把两边分的很不平衡，比如分成9:1或者8:2，在这种极端情况下快排的时间复杂度会退化到O(n2)。