CF115B Lawnmower

题目描述

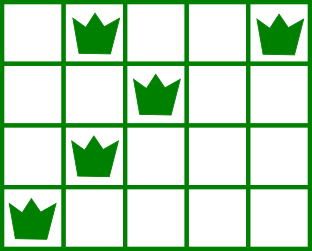
You have a garden consisting entirely of grass and weeds. Your garden is described by an n×mn×m grid, with rows numbered 11 to nn from top to bottom, and columns 11 to mm from left to right. Each cell is identified by a pair (r,c)(r,c)which means that the cell is located at row rr and column cc . Each cell may contain either grass or weeds. For example, a 4×54×5 garden may look as follows (empty cells denote grass):

You have a land-mower with you to mow all the weeds. Initially, you are standing with your lawnmower at the top-left corner of the garden. That is, at cell (1,1)(1,1) . At any moment of time you are facing a certain direction — either left or right. And initially, you face right.

In one move you can do either one of these:

1) Move one cell in the direction that you are facing.

• if you are facing right: move from cell (r,c)(r,c) to cell (r,c+1)(r,c+1) 

• if you are facing left: move from cell (r,c)(r,c) to cell (r,c-1)(r,c−1) 

  2) Move one cell down (that is, from cell (r,c)(r,c) to cell (r+1,c)(r+1,c) ), and change your direction to the opposite one.- if you were facing right previously, you will face left 

• if you were facing left previously, you will face right 

You are not allowed to leave the garden. Weeds will be mowed if you and your lawnmower are standing at the cell containing the weeds (your direction doesn't matter). This action isn't counted as a move.

What is the minimum number of moves required to mow all the weeds?

输入输出格式

输入格式：

The first line contains two integers nn and mm ( 1<=n,m<=1501<=n,m<=150 ) — the number of rows and columns respectively. Then follow nn lines containing mm characters each — the content of the grid. "G" means that this cell contains grass. "W" means that this cell contains weeds.

It is guaranteed that the top-left corner of the grid will contain grass.

输出格式：

Print a single number — the minimum number of moves required to mow all the weeds.

输入输出样例

输入样例#1：

4 5
GWGGW
GGWGG
GWGGG
WGGGG

输出样例#1：

11

输入样例#2：

3 3
GWW
WWW
WWG

输出样例#2：

7

输入样例#3：

1 1
G

输出样例#3：

0

说明

For the first example, this is the picture of the initial state of the grid:

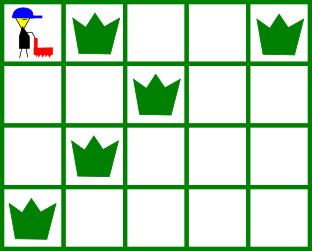A possible solution is by mowing the weeds as illustrated below:

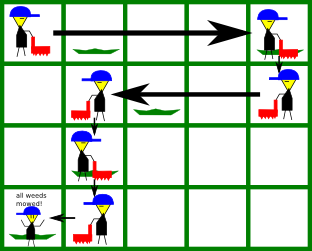
Solution：

　　本题比较水，直接贪心模拟就好了。

　　题意就是从$(1,1)$出发，最少需要多少步能除完草（即$W$），而每次移动的方向已经确定了，当$i$为奇数则第$i$行的方向为$1\rightarrow m$，否则为$m\rightarrow 1$，每次下移必须转变到所到行的方向上。

　　只需要记录一下每一行中草的位置，然后按行的方向模拟找到两边界（要么是一行草的开头位置，要么是结尾位置，具体由该行的方向确定），然后直接算曼哈顿距离，求和就解决了。

代码：

#include<bits/stdc++.h>
#pragma GCC optimize(2)
#define il inline
#define ll long long
#define For(i,a,b) for(int (i)=(a);(i)<=(b);(i)++)
#define Bor(i,a,b) for(int (i)=(b);(i)>=(a);(i)--)
using namespace std;
const int N=,M=;
int n,m,mp[N][N],cnt;
char s;
int main(){
    scanf("%d%d",&n,&m);
    For(i,,n) For(j,,m) {
        cin>>s;
        if(s=='W') mp[i][++mp[i][]]=j;
    }
    int ans=,lsx=,lsy=;
    For(i,,n) {
        if(i&) {
            if(mp[i][]){
                ans+=(abs(i-lsx)+abs(mp[i][]-lsy));
                ans+=(abs(mp[i][mp[i][]]-mp[i][]));
                lsx=i,lsy=mp[i][mp[i][]],cnt++;
            }
        }
        else {
            if(mp[i][]){
                ans+=(abs(i-lsx)+abs(mp[i][mp[i][]]-lsy));
                ans+=(abs(mp[i][mp[i][]]-mp[i][]));
                lsx=i,lsy=mp[i][],cnt++;
            }
        }
    }
    cout<<ans;
    return ;
}