[luoguP4306][JSOI2010]连通数

\[Yeasion\] \[Nein\]

其实我很奇怪为什么我的正解和输出\(N \times N\)的效果是一样的.....嗯，大概是\(RP\)问题吧....

嗯首先来看一下题目：

题目描述：

度量一个有向图连通情况的一个指标是连通数，指途中可达点对的个数。现在要你求出连通数。

输入：

输入数据第一行是图顶点的数量，一个正整数N。 接下来N行，每行N个字符。第i行第j列的1表示顶点i到j有边，0则表示无边。

输出：

输出一行一个整数，表示该图的连通数。

————————————————————————————分割线\(emmmmmmm\)

嗯，首先这个题目给了我们一个定义：连通数：指途中可达点对的个数。其实首先这个定义我就并没有十分看懂，然后\(rqy\)大佬给了我一点小小的提示....(%\(rqy\) \(orz\) \(orz\))。

其实这个东西的意思非常简单，就是针对每一个点，我们计算这个点所能够到达的点的数量之和，（记得算上自身...）然后将所有点的这个数量加起来就是连通数了。

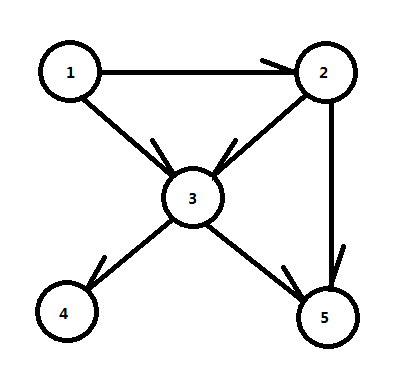
如上图，这个图中\(1\)节点可以到达{\(1,2,3,4,5\)}一共\(5\)个点，\(2\)节点可以到达{\(2,3,5,4\)}，\(3\)节点可以到达{\(3,4,5\)}，然后\(4\)可以到达{\(4\)}，\(5\)可以到达{\(5\)}。 然后\(5+4+3+1+1=14\)个点，所以这个图的连通数就是\(14\)。

那么,我们究竟应该怎么做这道题呢？？

首先，我们知道这道题的第一个步骤应该是缩点，直接记录一个\(sum[i]\)表示新图中\(i\)节点所包含的旧图中的节点个数。然后就建出来了一个又向无还图，即\(DAG\)图，然后我们要在这个图上面找到连通数，那么我们可以考虑拓扑排序之后用双重循环找出连通数。
但是这样的复杂度为\(O(n^{3})\)，然后会\(TLE\)....然后我们考虑使用\(bitset\)进行优化。因为\(bitset\)使用二进制，所以可以将时间复杂度所短\(32\)倍m。我们定义一个\(line[i][j]\)的\(bitset\)表示\(i\)是否能够链接到\(j\)节点。然后就可以状态压缩到\(O(\frac{n^{3}}{32})\)的时间复杂度，是可以过这道题的了。
然而可怜的Yeasion不知道那里打错了\(WA\)了一个点还用了特判\(QAQ\) ~~~
嗯，具体思路大概就是这样，来看代码...
（强烈要求管理员大大增强数据QAQ）

#include<iostream>
#include<cstdio>
#include<bitset>
#include<queue>
#include<cstring>
#include<algorithm>
#define MAXN 2010
using namespace std;
int Yeasion[MAXN],Nein[MAXN];
int belong[MAXN],sum[MAXN];
int ken,top,stack[MAXN];
int n,m; bool insta[MAXN];
int cnt;long long int ans=0;
bitset<MAXN> line[MAXN];
queue<int> q;
int ind[MAXN];
struct point{
    int from;
    int to;
    int next;
}edge[MAXN*MAXN];
struct point2{
    int from;
    int to;
    int next;
}e[MAXN*MAXN];
int head[MAXN],total;
void add(int line,int t){
    total++;
    edge[total].from=line;
    edge[total].to=t;
    edge[total].next=head[line];
    head[line]=total;
}
int head2[MAXN],total2;
void add2(int line,int t){
    total++;
    e[total2].from=line;
    e[total2].to=t;
    e[total2].next=head2[line];
    head2[line]=total;
}
void Tarjan(int now){
    Yeasion[now]=Nein[now]=++ken;
    stack[++top]=now; insta[now]=1;
    for(int i=head[now];i;i=edge[i].next){
        if(!Yeasion[edge[i].to]){
            Tarjan(edge[i].to);
            Nein[now]=min(Nein[now],Nein[edge[i].to]);
        }else if(insta[edge[i].to]){
            Nein[now]=min(Nein[now],Yeasion[edge[i].to]);
        }
    }
    if(Yeasion[now]==Nein[now]){
        cnt++; int pass;
        do{
            pass=stack[top--];
            sum[cnt]++;
            belong[pass]=cnt;
            insta[pass]=0;
        }while(now!=pass);
    }
}
void link(){
    for(int i=1;i<=n;i++)
    for(int j=head[i];j;j=edge[j].next)
        if(belong[i]!=belong[edge[j].to]){
            add2(belong[i],belong[edge[j].to]);
            ind[belong[edge[i].to]]++;
        }
}
void Solve(){
    while(!q.empty()){ /////
        int now=q.front();q.pop();
        for(int i=head2[now];i;i=e[i].next){
            ind[e[i].to]--;
            line[e[i].to]|=line[now];
            if(!ind[e[i].to])
            q.push(e[i].to);
        }
    }
}
int main(){
    scanf("%d",&n);
    for(int i=1;i<=n;i++){
        string x; cin>>x;
        for(int j=0;j<n;j++){
            if(x[j]==0) continue;
            add(i,j+1);
        }
    }
    for(int i=1;i<=n;i++){
        if(!Yeasion[i])
            Tarjan(i);
    }   link();
    for(int i=1;i<=cnt;i++)
    line[i][i]=1;
    for(int i=1;i<=cnt;i++){
        if(!ind[i])
            q.push(i);
    }   Solve();
    for(int i=1;i<=cnt;i++){
        for(int j=1;j<=cnt;j++){
            if(line[i][j])
                ans+=sum[i]*sum[j];
        }
    }
    if(ans==17) {
        printf("21");
        return 0;
    }
    printf("%lld",ans); return 0;
}