国密算法--Openssl 实现国密算法（加密和解密）

上一次讲了产生密钥，这次我们讲一下加密解密的实现。

先说一下加密解密的流程，一下这些内容都是从国密局发布的国密标准文档里面摘录出来的。大家可以去国密局的网站上自己下载。

下列符号适用于本部分。

A,B：使用公钥密码系统的两个用户。

a,b： Fq中的元素，它们定义Fq上的一条椭圆曲线E。

dB：用户B的私钥。

E(Fq)： Fq上椭圆曲线E 的所有有理点(包括无穷远点O)组成的集合。

Fq

：包含q个元素的有限域。

G：椭圆曲线的一个基点，其阶为素数。

2Hash( )：密码杂凑函数。

Hv

( )：消息摘要长度为v比特的密码杂凑函数。

KDF( )：密钥派生函数。

M ：待加密的消息。

M ′：解密得到的消息。

n：基点G的阶(n是# E(Fq)的素因子)。

O：椭圆曲线上的一个特殊点，称为无穷远点或零点，是椭圆曲线加法群的单位元。

PB：用户B的公钥。

q：有限域Fq中元素的数目。

x∥y： x与y的拼接，其中x、 y可以是比特串或字节串。

[k]P：椭圆曲线上点P的k倍点，即， [k]P= P + P + · · · + P(k个， k是正整数)。

[x,y]：大于或等于x且小于或等于y的整数的集合。

⌈x⌉：顶函数，大于或等于x的最小整数。例如⌈7⌉=7, ⌈8.3⌉=9。

⌊x⌋：底函数，小于或等于x的最大整数。例如⌊7⌋=7, ⌊8.3⌋=8。

E(Fq)： E(Fq)上点的数目，称为椭圆曲线E(Fq)的阶

下面给出加密过程：

设需要发送的消息为比特串M， klen为M的比特长度。

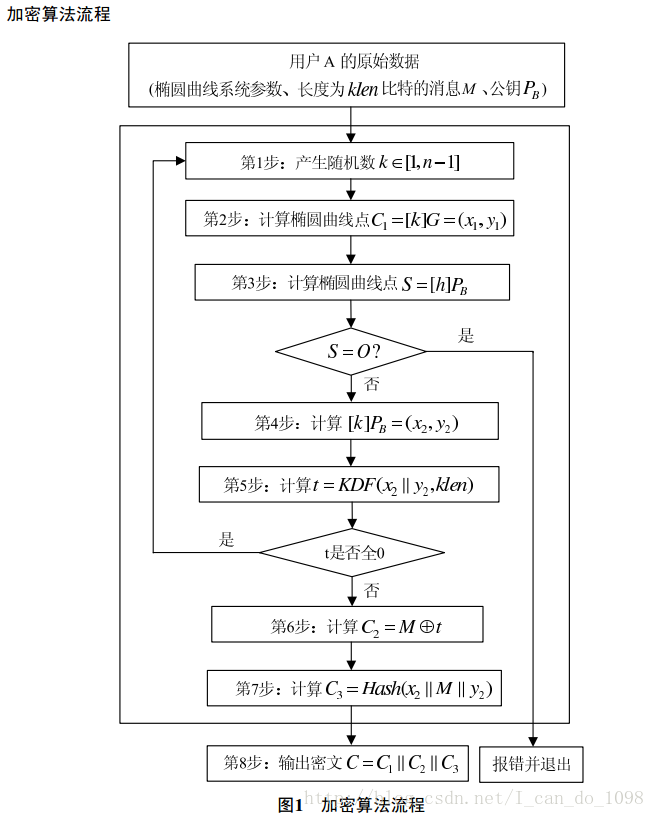
为了对明文M进行加密，作为加密者的用户A应实现以下运算步骤：

A1：用随机数发生器产生随机数k∈[1,n-1]；

A2：计算椭圆曲线点C1=[k]G=(x1,y1)，按本文本第1部分4.2.8和4.2.4给出的细节，将C1的数据类

型转换为比特串；

A3：计算椭圆曲线点S=[h]PB，若S是无穷远点，则报错并退出；

A4：计算椭圆曲线点[k]PB=(x2,y2)，按本文本第1部分4.2.5和4.2.4给出的细节，将坐标x2、 y2 的

数据类型转换为比特串；

A5：计算t=KDF(x2 ∥ y2, klen)，若t为全0比特串，则返回A1；

A6：计算C2 = M ⊕ t；

A7：计算C3 = Hash(x2 ∥ M ∥ y2)；

A8：输出密文C = C1 ∥ C2 ∥ C3。

以及加密流程图：

下面是加密的核心代码：

    unsigned char* t, *hm;
    BIGNUM* rand;
    EC_POINT* rG, *rK;
    BIGNUM *rKx, *rKy, *rGx, *rGy;

    unsigned char bK[65] = {0};
    unsigned char C3[33] = {0};

    rG = EC_POINT_new(this->mGroup);
    rK = EC_POINT_new(this->mGroup);
    rand = BN_new();

    //随机数k∈[1,n-1]
    BN_rand_range(rand, this->z);

    //C1=[k]G=(x1,y1)
    EC_POINT_mul(this->mGroup, rG, NULL,
        this->mGP, rand, this->ctx);

    rGx = BN_new();
    rGy = BN_new();
    if(!EC_POINT_get_affine_coordinates_GFp(this->mGroup,
        rG, rGx, rGy, this->ctx))
    {
        return -3;
    }

    BN_bn2bin(rGx, pd);
    BN_bn2bin(rGy, &pd[32]);

    //[k]PB=(x2,y2)
    EC_POINT_mul(this->mGroup, rK, NULL,
        EC_KEY_get0_public_key(this->mKey),
        rand, this->ctx);

    rKx = BN_new();
    rKy = BN_new();
    if(!EC_POINT_get_affine_coordinates_GFp(this->mGroup,
        rK, rKx, rKy, this->ctx))
    {
        return -3;
    }

    //t=KDF(x2||y2, klen)
    BN_bn2bin(rKx, bK);
    BN_bn2bin(rKy, &bK[32]);

    t = new BYTE[elen + 1];
    memset(t, 0, elen + 1);

    this->mKDF(bK, 64, elen, t);

    for (int i = elen; i--;)
    {
        t[i] = t[i]^pe[i];
    }

    //C3 = Hash(x2||M||y2)
    hm = new unsigned char[elen + 65];
    memset(hm, 0, elen + 65);

    memcpy(hm, bK, 32);
    memcpy(&hm[32], pe, elen);
    memcpy(&hm[elen + 32], &bK[32], 32);

    hash(hm, elen + 64, C3, "sha256");

    //C = C1||C2||C3
    memcpy(&pd[64], t,  elen);
    memcpy(&pd[64 + elen], C3, 32);

    delete[] t;
    delete[] hm;

    t = NULL;
    hm = NULL;

    EC_POINT_free(rG);
    EC_POINT_free(rK);

    return 0;

如果细心的朋友会发现我少了两步：

1.A3（校验rK这个点的）

2.校验 是否t为0

怎么说呢….因为我比较懒，而且也没有这个必要，因为我们用的是openssl，以上两种情况不会出现，所以就省略了，当然加上也无可厚非。

加密之后我们就要解密了，能拆就能立能砸就能砌。

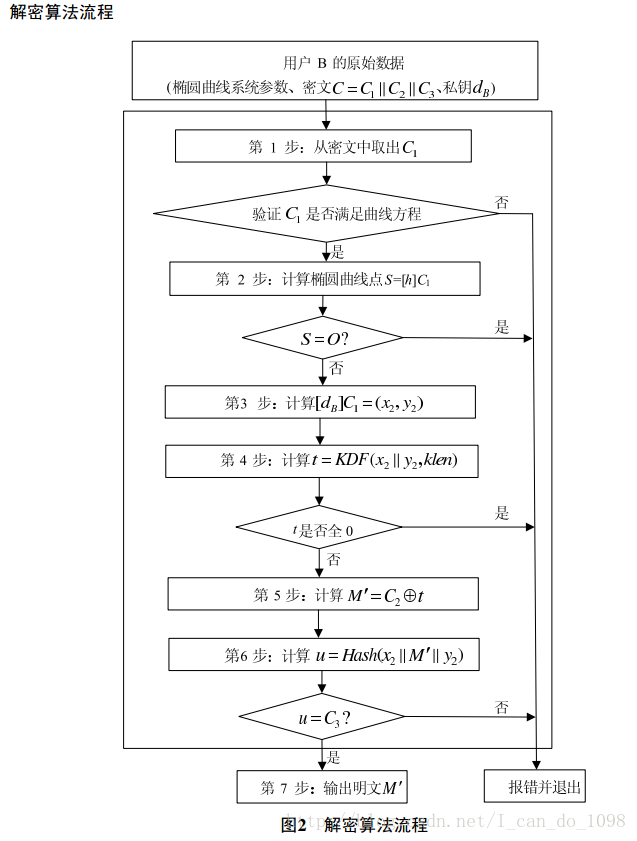
解密流程

解密算法

设klen为密文中C2的比特长度。

为了对密文C=C1 ∥ C2 ∥ C3 进行解密，作为解密者的用户B应实现以下运算步骤：

B1：从C中取出比特串C1，按本文本第1部分4.2.3和4.2.9给出的细节，将C1的数据类型转换为椭

圆曲线上的点，验证C1是否满足椭圆曲线方程，若不满足则报错并退出；

B2：计算椭圆曲线点S=[h]C1，若S是无穷远点，则报错并退出；

B3：计算[dB]C1=(x2,y2)，按本文本第1部分4.2.5和4.2.4给出的细节，将坐标x2、 y2的数据类型转

换为比特串；

B4：计算t=KDF(x2 ∥ y2, klen)，若t为全0比特串，则报错并退出；

B5：从C中取出比特串C2，计算M ′ = C2 ⊕ t；

B6：计算u = Hash(x2 ∥ M ′ ∥ y2)，从C中取出比特串C3，若u ̸= C3，则报错并退出；

B7：输出明文M ′。

以及解密流程图

下面是解密的核心代码：

unsigned char* t, *c2, *hm;
    unsigned char bC1x[65] = {0};
    unsigned char bC1y[65] = {0};
    unsigned char bK[65] = {0};
    unsigned char u[33] = {0}; 

    unsigned int mlen, hm_len;  

    EC_POINT *rG, *rK;
    BIGNUM *C1x, *C1y, *rKx, *rKy;

    //取出rG
    C1x = BN_new();
    C1y = BN_new();

    memcpy(&bC1x[32], pe, 32);
    memcpy(&bC1y[32], &pe[32], 32);

    BN_bin2bn(bC1x, 64, C1x);
    BN_bin2bn(bC1y, 64, C1y);

    rG = EC_POINT_new(this->mGroup);
    if(!EC_POINT_set_affine_coordinates_GFp(this->mGroup,
        rG, C1x, C1y, this->ctx))
    {
        EC_POINT_free(rG);
        return -1;
    }

    //求得rK
    rK = EC_POINT_new(this->mGroup);
    EC_POINT_mul(this->mGroup, rK, NULL, rG,
        EC_KEY_get0_private_key(this->mKey),
        this->ctx);

    rKx = BN_new();
    rKy = BN_new();
    if(!EC_POINT_get_affine_coordinates_GFp(this->mGroup,
        rK, rKx, rKy, this->ctx))
    {
        EC_POINT_free(rG);
        EC_POINT_free(rK);
        return -2;
    }

    //求取hv 解密
    BN_bn2bin(rKx, bK);
    BN_bn2bin(rKy, &bK[32]);

    mlen = elen - 96;

    c2 = new unsigned char[mlen + 1];
    memset(c2, 0, mlen + 1);
    memcpy(c2, &pe[64], mlen);

    t = new unsigned char[mlen + 1];
    memset(t, 0, mlen + 1);
    this->mKDF(bK, 64, elen - 96, t);

    for (int i = elen - 96; i--;)
    {
        t[i] = t[i]^c2[i];
    }

    hm_len = mlen + 64;
    hm = new unsigned char[hm_len + 1];
    memset(hm, 0,hm_len + 1);

    BN_bn2bin(rKx, hm);
    memcpy(&hm[32], t, mlen);
    BN_bn2bin(rKy, &hm[32 + mlen]);

    //校验hash值
    hash(hm, hm_len, u, "sha256");
    for (int i = 0; i < 32;i++)
    {
        if (u[i] != pe[elen - 32 + i])
        {
            EC_POINT_free(rG);
            EC_POINT_free(rK);

            delete[] t;
            delete[] c2;
            delete[] hm;

            t = NULL;
            c2 = NULL;
            hm = NULL;

            return -3;
        }
    }

    memcpy(pd, t, mlen);

    EC_POINT_free(rG);
    EC_POINT_free(rK);

    delete[] t;
    delete[] c2;
    delete[] hm;

    t = NULL;
    c2 = NULL;
    hm = NULL;

    return 0;

以上就是加解密的过程，完整代码我会上传到github上面.