[IOI2011]Race

2599: [IOI2011]Race

Time Limit: 70 Sec  Memory Limit: 128 MB
http://www.lydsy.com/JudgeOnline/problem.php?id=2599

Description

给一棵树,每条边有权.求一条简单路径,权值和等于K,且边的数量最小.N <= 200000, K <= 1000000

Input

第一行 两个整数 n, k
第二..n行 每行三个整数 表示一条无向边的两端和权值 (注意点的编号从0开始)

Output

一个整数 表示最小边数量 如果不存在这样的路径 输出-1

Sample Input

4 3
0 1 1
1 2 2
1 3 4

Sample Output

2

点分治

poj 1741http://www.cnblogs.com/TheRoadToTheGold/p/6378840.html

是求两点间边权和<=k的数量

这里是求两点间边权和=k的最少边数

我们仍然可以借用上题的方法，多记录一个节点到根节点的经过的边数即可

有2个地方需要修改：

① 上题需要减去同一子树中不合法的点对个数

    本题虽不需要考虑同一子树内的情况，但需要在计算时跳过同一子树内的2个点

    具体做法是 在递归记录点与根节点间权值和、边数时，顺带记录每个点属于 当前根节点的哪颗子树

     计算时，如果属于同一子树，跳过

    代码：

　　if(fa==head||!fa) deep[deep[0].edge_sum].id=x;

　　else deep[deep[0].edge_sum].id=deep[deep[0].edge_sum-1].id;

当前点为x，head表示当前根节点下的哪颗子树，fa表示x的父节点，id记录当前点属于哪颗子树

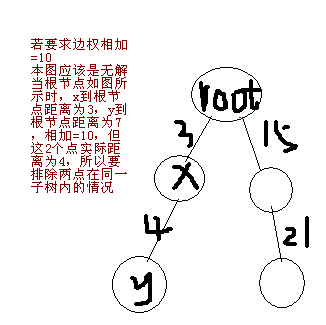
上题能不能采用同样的方法，避免计算子树内部的情况呢？

不能。因为排序仅按边权大小排，累计答案的方式是加r-l，即一堆满足条件的点判断一次，一起累加。

判断的两个点在同一子树内，其他的点可能不在同一子树内

②统计答案的时候，仍然可以同上题一样采用两边指针向中间逼近的方式

但要特殊处理指针指向位置周围边权相等的情况

 

#include<cstdio>
#include<algorithm>
#define N 200001
using namespace std;
int n,k,tot,sum,root,son[N],f[N],d[N],ans=N;
int front[N],to[N*],next[N*],w[N*];
bool v[N];
struct node
{
    int dis,edge_sum,id;
}deep[N];
void getroot(int x,int fa)
{
    son[x]=;f[x]=;
    for(int i=front[x];i;i=next[i])
    {
        if(to[i]==fa||v[to[i]]) continue;
        getroot(to[i],x);
        son[x]+=son[to[i]];
        f[x]=max(f[x],son[to[i]]);
    }
    f[x]=max(f[x],sum-son[x]);
    if(f[x]<f[root]) root=x;
}
void getdeep(int head,int x,int fa,int edge_sum)
{
    deep[++deep[].edge_sum]=(node){d[x],edge_sum};
    if(fa==head||!fa) deep[deep[].edge_sum].id=x;
    else deep[deep[].edge_sum].id=deep[deep[].edge_sum-].id;
    for(int i=front[x];i;i=next[i])
    {
        if(v[to[i]]||to[i]==fa) continue;
        d[to[i]]=d[x]+w[i];
        getdeep(head,to[i],x,edge_sum+);
    }
}
bool cmp(node l,node r)
{
    /*if(l.dis!=r.dis) return l.dis<r.dis;
    return l.edge_sum>r.edge_sum;*/
    return l.dis<r.dis;
}
void cal(int x,int now)
{
    d[x]=now;deep[].edge_sum=;
    getdeep(x,x,,);
    int l=,r=deep[].edge_sum,t=;
    sort(deep+,deep+r+,cmp);
    while(l<r)
    {
        /*if(deep[l].dis+deep[r].dis==k&&deep[l].id!=deep[r].id)
        {
            ans=min(ans,deep[l].edge_sum+deep[r].edge_sum);
            //printf("%d %d\n",deep[l].dis,deep[r].dis);
            l++;

        }*/   //  错误的
        if(deep[l].dis+deep[r].dis==k)
        {
            int p1=l,p2=r;
            while(deep[p1].dis+deep[r].dis==k) p1++;p1--;
            while(deep[p2].dis+deep[l].dis==k) p2--;p2++;
            for(int i=l;i<=p1;i++)
             for(int j=p2;j<=r;j++)
              if(deep[i].id!=deep[j].id)
               ans=min(ans,deep[i].edge_sum+deep[j].edge_sum);
            l=p1+;r=p2-;
        }
        else if(deep[l].dis+deep[r].dis<k) l++;
        else r--;
    }
}
void work(int x)
{
    cal(x,);
    v[x]=true;
    for(int i=front[x];i;i=next[i])
    {
        if(v[to[i]]) continue;
        sum=son[to[i]];
        root=;
        getroot(to[i],root);
        work(root);
    }
}
void add(int u,int v,int val)
{
    to[++tot]=v;next[tot]=front[u];front[u]=tot;w[tot]=val;
    to[++tot]=u;next[tot]=front[v];front[v]=tot;w[tot]=val;
}
int read()
{
    int x=,f=;char c=getchar();
    while(c<''||c>'') {if(c=='-') f=-;c=getchar();}
    while(c>=''&&c<='') {x=x*+c-'';c=getchar();}
    return x*f;
}
int main()
{
    n=read();k=read();
    int x,y,z;
    for(int i=;i<n;i++)
    {
        x=read();y=read();z=read();
        x++;y++;
        add(x,y,z);
    }
    f[]=N;
    sum=n;
    getroot(,);
    work(root);
    printf("%d",ans==N ? -:ans);
}