【ARC075F】Mirror

Description

　　

​　　 给定正整数\(D\)，求有多少个正整数\(N\)，满足\(rev(N)=N+D\)。

　　

​　　 其中\(rev(N)\)表示将\(N\)的十进制表示翻转来读得到的数（翻转后忽略前导零）。

　　

​　　 答案对\(10^9+7\)取模。

　　

​　　 \(D \le 10^{9}\)

　　

　　（实际可以做到\(D \le 10^{5000}\)）

　　

　　

　　

Solution

　　

　　​ 原题\(D \le 10^9\)，暴力可过；但DP做法可以应用到更大的范围。

　　

　　​

　　

　　​ 考虑枚举\(N\)有多少位，记为\(len\)。

　　

​　　 显然\(len\)不能小于\(D\)的位数，否则一定不合法。并且可以证明，\(len\)超过\(D\)的位数的两倍时，就没有数合法了。再者\(len==1\)的时候也显然不合法。所以枚举区间是\([\max (2,|D|),2|D|]\)。

　　

​　　 设计一个DP来计算在\(N\)的长度为\(len\)时，有多少个数满足条件。

　　

​　　 把和式画出来，并从两端向中间标号：

　　



　　

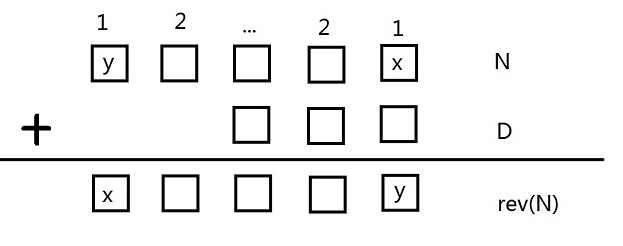
​　　 为什么要这么标号？因为既然是翻转，所以确定一组中的一对数\((x,y)\)就可以确定另一对数\((y,x)\)。

　　

​　　 还要考虑进位问题，那么状态里应该有表示进位的东西。

　　

​　　 设\(f_{i,j,k}\)表示第\(i\)组数，其中左边一组数从其右边有无收到进位（\(j=0,1\)），且右边一组数给其左边有无进位（\(k=0,1\)）：

　　

​　　

　　

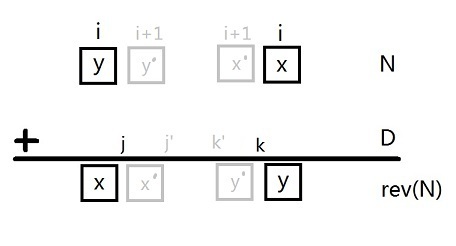
​　　 枚举状态\(f_{i,j,k}\)，正向转移到可去的状态。枚举\(i+1\)组的\(x'\)选0...9，并通过右边一组数的\(k\)和相应位置的\(D\)的数位算出\(y''\)与\(k'\)。再用左边一组数的\(j\)来计算出\(j'\)。如果\(j'<0\)或者\(j'>1\)就说明这个转移不合法，舍弃。因此，每个\(x\)的取值对应了唯一对应（有可能不合法，舍弃）的新状态\(f_{i+1,j',k'}\)，将方案数加上即可。

　　

​　　 注意第1组数的\(x\)不可以选0，不然会违背当前正在考虑长度为\(len\)的\(N\)这个前提。

　　

​　　 如果\(len\)是偶数，那么对于\(i=1..\frac{len}{2}\)计算\(f\)，答案即为\(f_{\frac{len}2,0,0}+f_{\frac{len}2,1,1}\)

　　

​　　 如果\(len\)是奇数，则先对于\(i=1...\lfloor \frac{len}2 \rfloor\)计算\(f\)，先枚举每个最终状态，再枚举最中间一位选择\(0...9\)，是否能满足各个进位与否的要求，统计进答案即可。

　　

​　　

　　

​　　 总时间复杂度\(\mathcal O(\frac{|D|^2}2*10*2*2)=\mathcal O(|D|^220)\)，基本上不会跑满。我造数据时测了一下5000可以秒出，题目就开了5000的长度；然后我SUODCX后构造了一组特殊数据，使得\(N\)长度恰好是\(2|D|\)时也有解，几乎把复杂度卡满了，所以这个点只开到了3000（已经可以跑得出了）.

　　

　　

　　　

Code

　　

c++
#include <cstdio>
#include <cstring>
using namespace std;
const int N=10010,MOD=1e9+7;
int d[N];
int f[N][2][2];
inline int max(int x,int y){
	return x>y?x:y;
}
void readData(){
	static char str[N];
	scanf("%s",str+1);
	d[0]=strlen(str+1);
	for(int i=1;i<=d[0];i++) d[d[0]-i+1]=str[i]-'0';
}
int dp(int n){
	int m=n>>1;
	for(int i=0;i<=m;i++)
		for(int j=0;j<2;j++)
			for(int k=0;k<2;k++)
				f[i][j][k]=0;
	f[0][0][0]=1;
	for(int i=0;i<m;i++)
		for(int j=0;j<2;j++)
			for(int k=0;k<2;k++)
				if(f[i][j][k]){
					for(int x=0,y,j1,k1;x<10;x++){
						k1=x+d[i+1]+k;
						y=k1%10;
						k1/=10;
						j1=10*j+x-y-d[n-i];
						if(j1<0||j1>1) continue;
						if(!i&&(!x||!y)) continue;
						(f[i+1][j1][k1]+=f[i][j][k])%=MOD;
					}
				}
	int res=0;
	if(n&1){
		int mid=(n+1)>>1;
		for(int j=0;j<2;j++)
			for(int k=0;k<2;k++)
				if(f[m][j][k])
					for(int x=0,y;x<10;x++){
						y=x+d[mid]+k;
						if((x==y%10)&&(y/10==j))
							(res+=f[m][j][k])%=MOD;
					}
	}
	else{
		for(int j=0;j<2;j++)
			(res+=f[m][j][j])%=MOD;
	}
	return res;
}
void solve(){
	int ans=0,maxlen=d[0]<<1;
	for(int i=max(2,d[0]);i<=maxlen;i++)
		(ans+=dp(i))%=MOD;
	printf("%d\n",ans<0?ans+MOD:ans);
}
int main(){
	readData();
	solve();
	return 0;
}