【Codeforces528D】Fuzzy Search FFT

D. Fuzzy Search

time limit per test：3 seconds

memory limit per test：256 megabytes

input：standard input

output：standard output

Leonid works for a small and promising start-up that works on decoding the human genome. His duties include solving complex problems of finding certain patterns in long strings consisting of letters 'A', 'T', 'G' and 'C'.

Let's consider the following scenario. There is a fragment of a human DNA chain, recorded as a string S. To analyze the fragment, you need to find all occurrences of string T in a string S. However, the matter is complicated by the fact that the original chain fragment could contain minor mutations, which, however, complicate the task of finding a fragment. Leonid proposed the following approach to solve this problem.

Let's write down integer k ≥ 0 — the error threshold. We will say that string T occurs in string S on position i (1 ≤ i ≤ |S| - |T| + 1), if after putting string T along with this position, each character of string T corresponds to the some character of the same value in string S at the distance of at most k. More formally, for any j (1 ≤ j ≤ |T|) there must exist such p (1 ≤ p ≤ |S|), that |(i + j - 1) - p| ≤ k and S[p] = T[j].

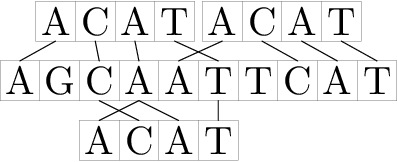
For example, corresponding to the given definition, string "ACAT" occurs in string "AGCAATTCAT" in positions 2, 3 and 6.

Note that at k = 0 the given definition transforms to a simple definition of the occurrence of a string in a string.

Help Leonid by calculating in how many positions the given string T occurs in the given string S with the given error threshold.

Input

The first line contains three integers |S|, |T|, k (1 ≤ |T| ≤ |S| ≤ 200 000, 0 ≤ k ≤ 200 000) — the lengths of strings S and T and the error threshold.

The second line contains string S.

The third line contains string T.

Both strings consist only of uppercase letters 'A', 'T', 'G' and 'C'.

Output

Print a single number — the number of occurrences of T in S with the error threshold k by the given definition.

Examples

input

10 4 1
AGCAATTCAT
ACAT

output

3

Note

If you happen to know about the structure of the human genome a little more than the author of the problem, and you are not impressed with Leonid's original approach, do not take everything described above seriously.

Solution

题目大意:给出A,B串，求B串在A串中出现的次数.这里的A串有奇怪的性质，对于一个位置$i$，只要$[i-k,i+k]$中存在合法匹配B中一个字符，则可以认为$i$位置匹配。字符集大小AGCT

毛啸论文里的例题，FFT的简单应用。 详细的看论文吧..

Code

#include<iostream>
#include<cstdio>
#include<cmath>
#include<algorithm>
#include<cstring>
#include<map>
using namespace std;
#define MAXN 800010
#define Pai acos(-1.0)
map<char,int>id;
char a[MAXN],b[MAXN];
int ok[MAXN][5],cnt[5],N,M,K,ans[MAXN],len;
struct Complex{
	double r,i;
	Complex (double R=0.0,double I=0.0) {r=R,i=I;}
	Complex operator + (const Complex & A) const {return Complex(r+A.r,i+A.i);}
	Complex operator - (const Complex & A) const {return Complex(r-A.r,i-A.i);}
	Complex operator * (const Complex & A) const {return Complex(r*A.r-i*A.i,r*A.i+i*A.r);}
};
Complex A[MAXN],B[MAXN],C[MAXN];
inline void Prework(int j)
{
	len=1;
	while (len<(N<<1)) len<<=1;
	for (int i=0; i<N; i++) A[i]=Complex(ok[i+1][j],0);
	for (int i=N; i<len; i++) A[i]=Complex(0,0);
//	for (int i=0; i<len; i++) printf("%d  ",(int)(A[i].r+0.5)); puts("");
	for (int i=0; i<M; i++) B[i]=Complex(id[b[M-i]]==j,0);
	for (int i=M; i<len; i++) B[i]=Complex(0,0);
//	for (int i=0; i<len; i++) printf("%d  ",(int)(B[i].r+0.5)); puts("");
}
inline void Rader(Complex *x)
{
	for (int i=1,j=len>>1,k; i<len-1; i++)
		{
			if (i<j) swap(x[i],x[j]);
			k=len>>1;
			while (j>=k) j-=k,k>>=1;
			if (j<k) j+=k;
		}
}
inline void DFT(Complex *x,int opt)
{
	Rader(x);
	for (int h=2; h<=len; h<<=1)
		{
			Complex Wn( cos(opt*2*Pai/h) , sin(opt*2*Pai/h) );
			for (int i=0; i<len; i+=h)
				{
					Complex W(1,0);
					for (int j=i; j<i+h/2; j++)
						{
							Complex u=x[j],t=x[j+h/2]*W;
							x[j]=u+t; x[j+h/2]=u-t;
							W=W*Wn;
						}
				}
		}
	if (opt==-1)
		for (int i=0; i<len; i++) x[i].r/=len;
}
inline void FFT(Complex *A,Complex *B,Complex *C)
{
	DFT(A,1); DFT(B,1);
	for (int i=0; i<len; i++) C[i]=A[i]*B[i];
	DFT(C,-1);
	for (int i=0; i<len; i++) ans[i]+=(int)(C[i].r+0.5);
}
int main()
{
	id['A']=1,id['G']=2,id['C']=3,id['T']=4;
	scanf("%d%d%d%s%s",&N,&M,&K,a+1,b+1);
	int l=0,r=0;
	for (int i=1; i<=N; i++)
		{
			while (l<N && l<i-K) cnt[id[a[l++]]]--;
			while (r<N && r<i+K) cnt[id[a[++r]]]++;
			for (int j=1; j<=4; j++) if (cnt[j]) ok[i][j]=1;
		}
//	for (int i=1; i<=N; i++) printf("%d  %d  %d  %d\n",ok[i][1],ok[i][2],ok[i][3],ok[i][4]);
	for (int j=1; j<=4; j++) Prework(j),FFT(A,B,C);
	int Ans=0;
	for (int i=0; i<len; i++) if (ans[i]==M) Ans++;
	printf("%d\n",Ans);
	return 0;
}