一.下载欢乐捕鱼的素材包

https://files.cnblogs.com/files/wordblog/%E7%B4%A0%E6%9D%90.zip

二.把欢乐捕鱼素材放入项目中 并启动tomcat

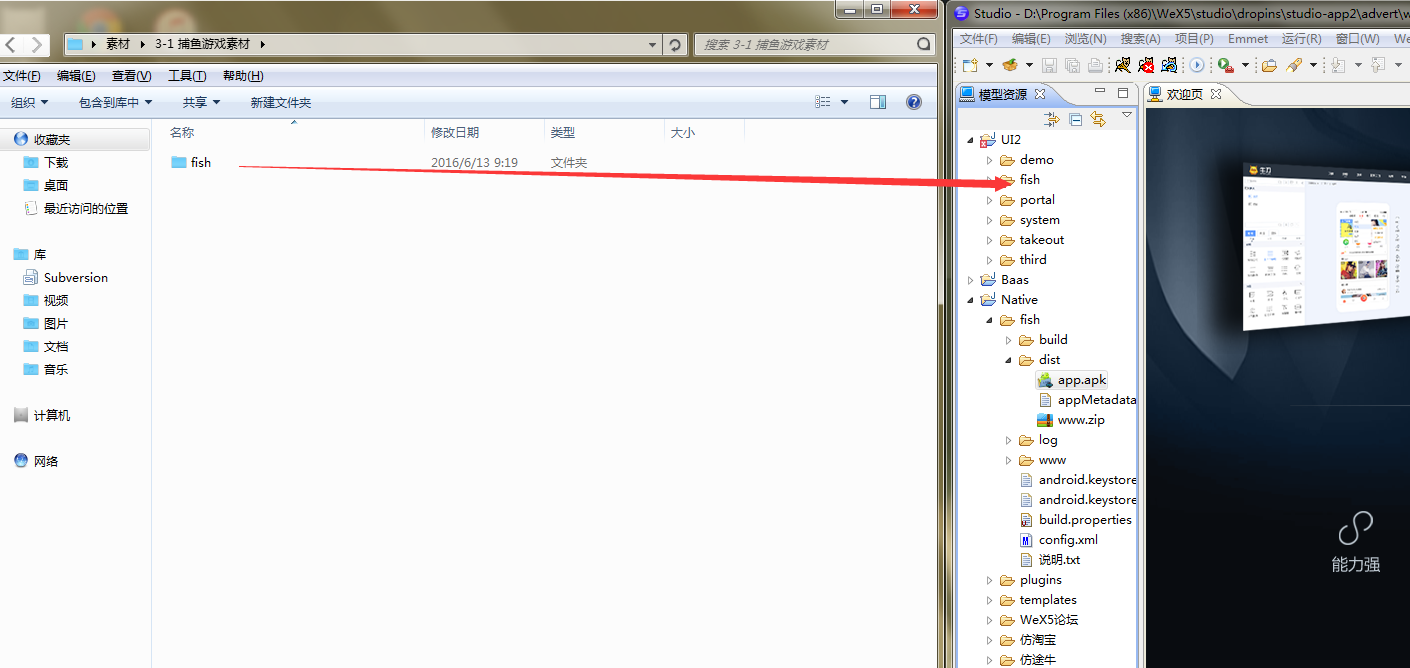
三.打包

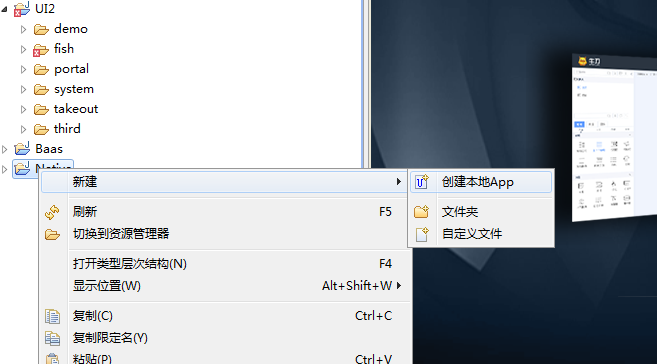
在native目录上右键创建本地APP

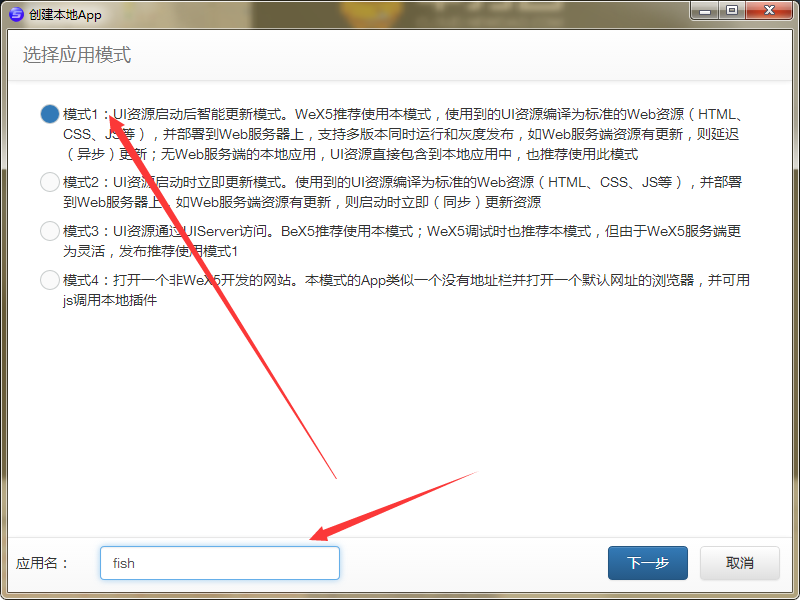
填入应用名 选择第一个模式

填入欢乐捕鱼的默认首页地址 并选择fish资源目录

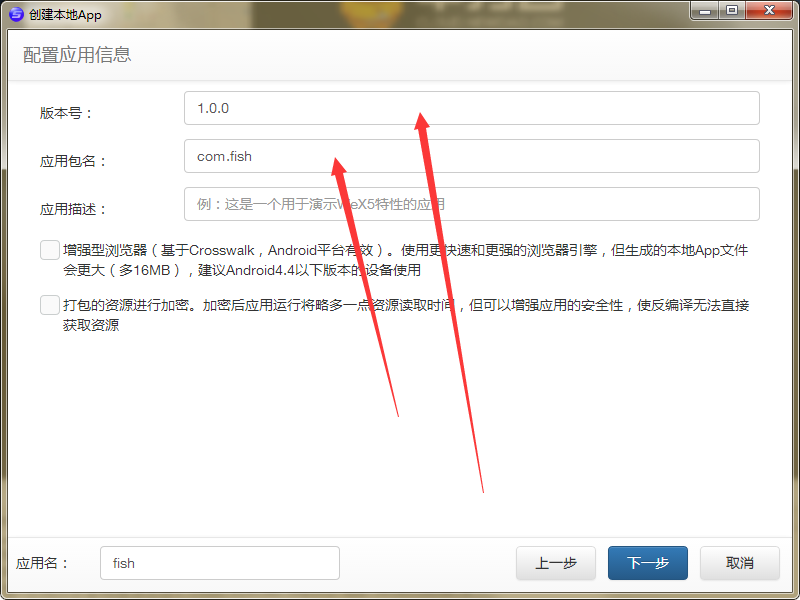
版本号和包名填好

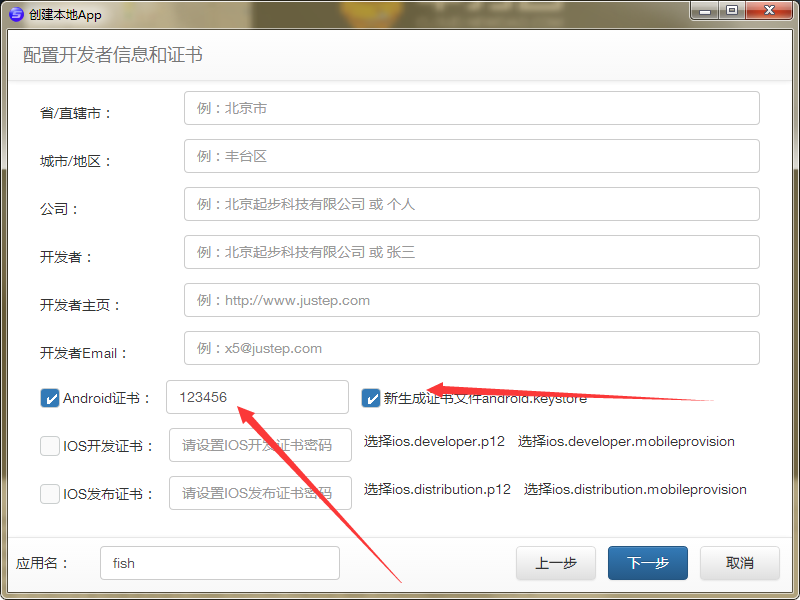
windows上只能打安卓包 填入密码 勾选新生成证书

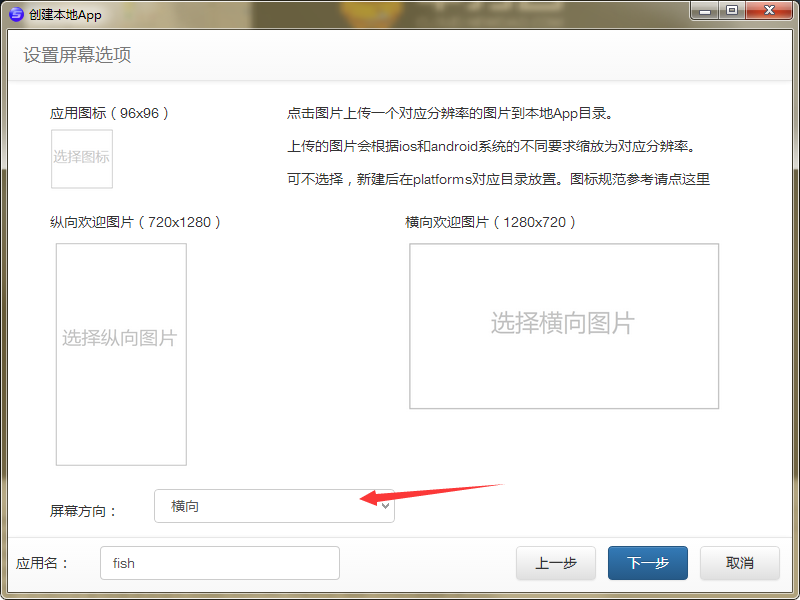
横向 其他默认

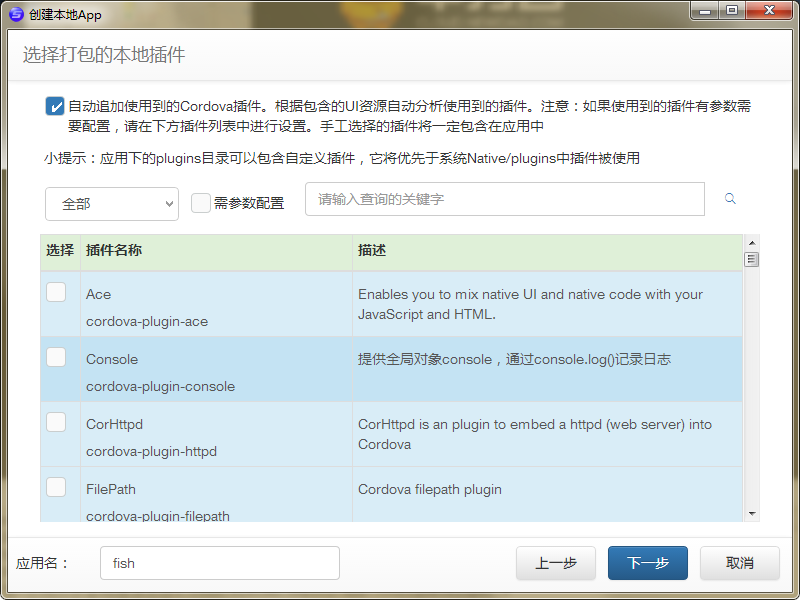
默认即可

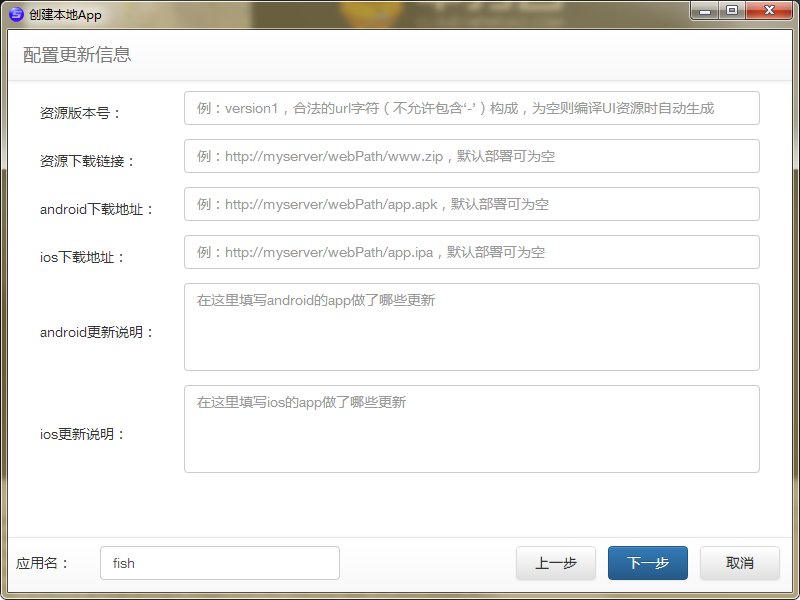
同上

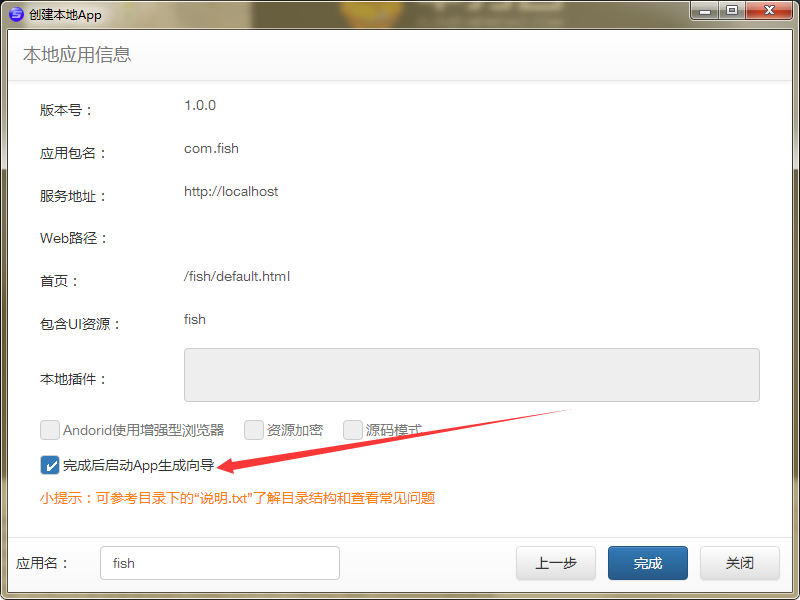
重要 勾上这个

开始打包了

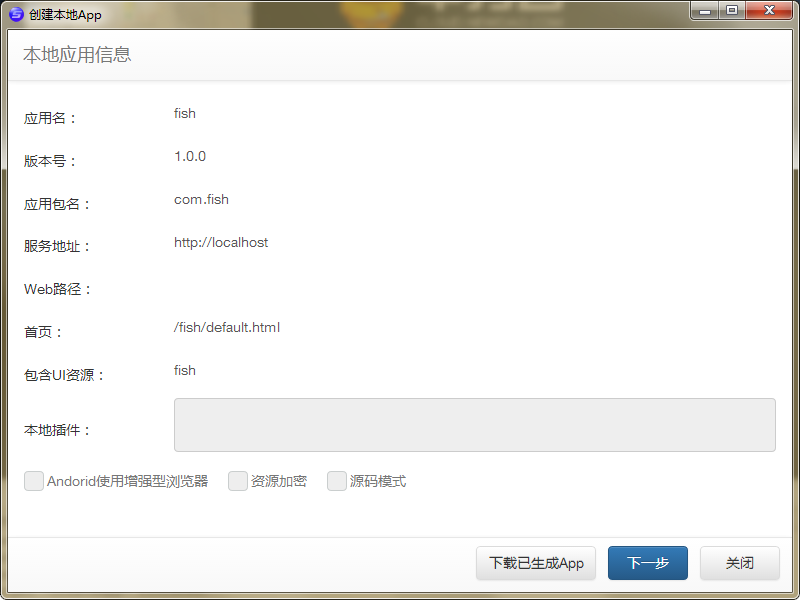
点下一步

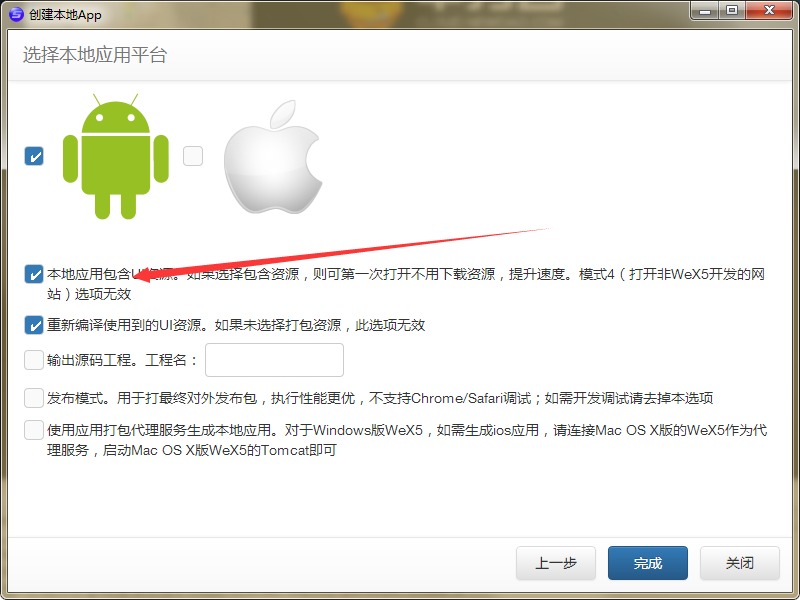
勾上这个 其他默认 点完成 这里如果连接打包服务器失败 看这篇文章：https://www.cnblogs.com/yingmeng/p/5856912.html

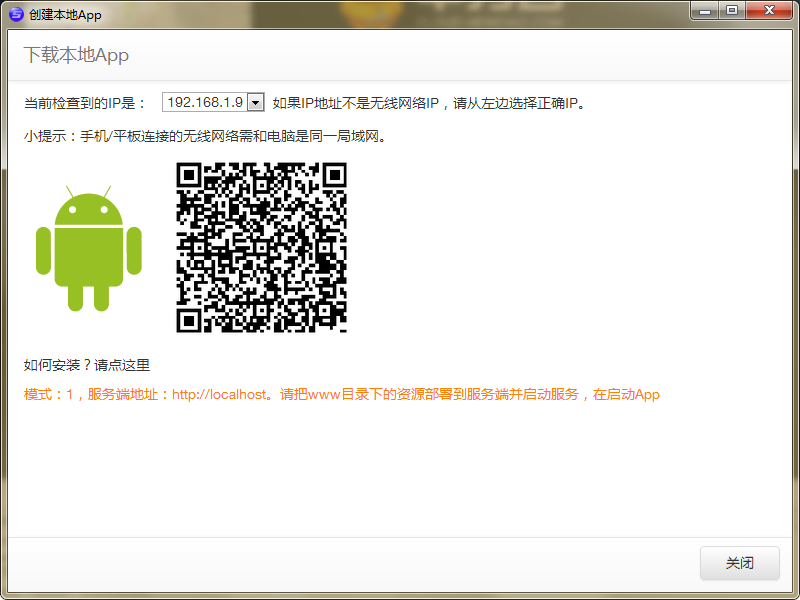
经过漫长等待 出现这个界面 表示打包完成 你可以扫码下载 也可以到下面：

这个就是打包后的APK文件了 可以放手机或者模拟器上运行了

这是在模拟器里运行的情况

谢谢观看！

WeX5入门之欢乐捕鱼打包的更多相关文章

  1. 。。。欢乐捕鱼App WeX5 连接打包代理服务失败，请检查代理服务地址是否正确。。。

    今天学习了WeX5,第一次使用,使用它打包一个Web App 欢乐捕鱼的时候,在最终打包生成Native App的时候突然报错了,说:"连接打包代理服务失败,请检查代理服务地址是否正确&qu ...

  2. 【转】Python3 (入门6) 库的打包与安装

    Python3 (入门6) 库的打包与安装 本文由 Luzhuo 编写,转发请保留该信息. 原文: http://blog.csdn.net/Rozol/article/details/6940288 ...

  3. cocos2d-x 欢乐捕鱼游戏总结

    这几天一直都在做一个捕鱼游戏Demo,大概花掉了我快一个礼拜的时间.游戏主体是使用的cocos2d-x高级开发教程里面提供的小部分框架基本功能.然后自己加入所有的UI元素和玩法.变成了一个体验不错的捕 ...

  4. ANE 从入门到精通 --- 一键打包ANE

    每次都要执行好几步才能编译出ANE很是麻烦,使用如下脚本 一键完成复杂的流程 REM 好压HaoZipC文件所在的位置,7Zip,WinRAR等均可 Set Zip=D:\"Program ...

  5. Webpack 入门(一)：安装 / 打包 / 命令行

    一:安装webpack和基本环境搭建 新建一个工作的文件夹(我取的名字叫Webpack) 打开命令行,cd进入该文件夹 //初始化一下npm > E:\work\Webpack>npm i ...

  6. WeX5入门之HelloWorld

    学习目标:数据双向绑定 在ui2上右键 新建一个应用 然后会出现一个目录 右键hello 在创建页面 选择标准的空白模板 并起一个名 自动生成这两个文件 建立一个input组件 再建一个output组 ...

  7. WeX5开发指南

    WeX5入门.UI2开发.App开发.服务端开发.扩展资料学习. 1 新手入门 1.1 运行WeX5的demo(视频) 1.2 App开发.调试.打包部署完整过程(视频) 1.3 创建第一个应用(视频 ...

  8. WeX5学习笔记

    目录 WeX5学习笔记... 1 1.轻松看透WeX5产品能力和技术... 1 2.WeX5可以怎么玩?... 3 一.纯本地App. 3 二.关联一个网站,希望默认就打开某页... 4 三.UI设计 ...

  9. ANE 从入门到精通 --- 使用R* 访问资源

    在AIR4.0版本之前,ANE内无法使用R*,操作资源仅能使用getResourceID(). 对于接SDK来说尤为头疼. 不过4.0以后可以通过在打包时候指定platform.xml来直接使用R*访 ...

随机推荐

  1. SpringBoot(九)_springboot集成 MyBatis

    MyBatis 是一款标准的 ORM 框架,被广泛的应用于各企业开发中.具体细节这里就不在叙述,大家自行查找资料进行学习下. 加载依赖 <dependency> <groupId&g ...

  2. 用java和junit编写app自动化测试用例

    package myTest; import static org.junit.Assert.*; import io.appium.java_client.android.AndroidDriver ...

  3. BZOJ1064 NOI2008假面舞会（dfs树）

    将图中的环的长度定义为正向边数量-反向边数量,那么答案一定是所有环的环长的共同因子.dfs一下就能找到图中的一些环,并且图中的所有环的环长都可以由这些环长加加减减得到(好像不太会证).如果有环长为1或 ...

  4. [BZOJ2095][Poi2010]Bridges 最大流（混合图欧拉回路）

    2095: [Poi2010]Bridges Time Limit: 10 Sec  Memory Limit: 259 MB Description YYD为了减肥,他来到了瘦海,这是一个巨大的海, ...

  5. 【刷题】UOJ #207 共价大爷游长沙

    火车司机出秦川,跳蚤国王下江南,共价大爷游长沙.每个周末,勤劳的共价大爷都会开车游历长沙市. 长沙市的交通线路可以抽象成为一个 \(n\) 个点 \(n−1\) 条边的无向图,点编号为 \(1\) 到 ...

  6. 注册系统所有的dll文件.bat

    @echo off echo 运行后,能重新注册系统所有的dll文件, echo 能解决内存读写错误的问题 pause echo on for %%1 in (%windir%/system32/*. ...

  7. Metasploit+python生成免杀exe过360杀毒

    Metasploit+python生成免杀exe过360杀毒 1在kali下生成一个反弹的msf的python脚本,命令如下: msfvenom -p windows/meterpreter/reve ...

  8. 导入eclipse工程到Android Studio中

    ref:从 Eclipse 迁移至 Android Studio | Android Studiohttps://developer.android.com/studio/intro/migrate. ...

  9. boost::asio::deadline_timer(理解)

    并发与并行: 并发和并行从宏观上来讲都是同时处理多路请求的概念.但并发和并行又有区别,并行是指两个或者多个事件在同一时刻发生:而并发是指两个或多个事件在同一时间间隔内发生. 1.Timer.1 - 使 ...

  10. idea中复制module和module中的蓝色tag出现的方法

    1.在从github上面导入项目到idea中时,经常好多module都是没有蓝色的tag的,这说明这不是个maven形式的module,需要导入到项目中. 举个例子: 有蓝色tag的module才可以 ...