洛谷——P1231 教辅的组成

P1231 教辅的组成

题目背景

滚粗了的HansBug在收拾旧语文书，然而他发现了什么奇妙的东西。

题目描述

蒟蒻HansBug在一本语文书里面发现了一本答案，然而他却明明记得这书应该还包含一份练习题。然而出现在他眼前的书多得数不胜数，其中有书，有答案，有练习册。已知一个完整的书册均应该包含且仅包含一本书、一本练习册和一份答案，然而现在全都乱做了一团。许多书上面的字迹都已经模糊了，然而HansBug还是可以大致判断这是一本书还是练习册或答案，并且能够大致知道一本书和答案以及一本书和练习册的对应关系（即仅仅知道某书和某答案、某书和某练习册有可能相对应，除此以外的均不可能对应）。既然如此，HansBug想知道在这样的情况下，最多可能同时组合成多少个完整的书册。

输入输出格式

输入格式：

第一行包含三个正整数N1、N2、N3，分别表示书的个数、练习册的个数和答案的个数。

第二行包含一个正整数M1，表示书和练习册可能的对应关系个数。

接下来M1行每行包含两个正整数x、y，表示第x本书和第y本练习册可能对应。（1<=x<=N1，1<=y<=N2）

第M1+3行包含一个正整数M2，表述书和答案可能的对应关系个数。

接下来M2行每行包含两个正整数x、y，表示第x本书和第y本答案可能对应。（1<=x<=N1，1<=y<=N3）

输出格式：

输出包含一个正整数，表示最多可能组成完整书册的数目。

输入输出样例

输入样例#1： 复制

5 3 4
5
4 3
2 2
5 2
5 1
5 3
5
1 3
3 1
2 2
3 3
4 3

输出样例#1： 复制

2

说明

样例说明：

如题，N1=5，N2=3，N3=4，表示书有5本、练习册有3本、答案有4本。

M1=5，表示书和练习册共有5个可能的对应关系，分别为：书4和练习册3、书2和练习册2、书5和练习册2、书5和练习册1以及书5和练习册3。

M2=5，表示数和答案共有5个可能的对应关系，分别为：书1和答案3、书3和答案1、书2和答案2、书3和答案3以及书4和答案3。

所以，以上情况的话最多可以同时配成两个书册，分别为：书2+练习册2+答案2、书4+练习册3+答案3。

数据规模：

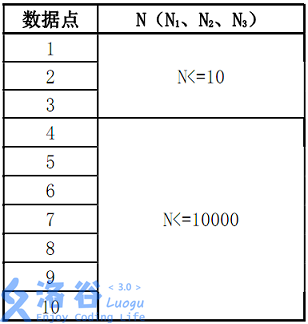
对于数据点1, 2, 3，M1，M2<= 20

对于数据点4~10，M1，M2 <= 20000

相信大佬们一眼就能看出来这是个网络流最大流的模板题吧。

怎么做？直接把每一个点都连起来跑最大流？

有没有注意到这个题每一本书只能用一次？这样的话要怎么办？

有人就会说了，这个好办，把所有的边的流量都赋成1不就行了吗？

额额，好像很有道理的样子，但是对于这样一个图，

1 2 2

2

1 1

1 2

2

1 1

1 2

如果我们对他跑最大流的话，我们的结果会是2但实际应该是1，纵使我们把所有的边权都赋成1最后的结果还是2，那么我们要怎么办呢？这个时候有人就会说了，拆点啊

我们将中间的点拆成两个，然后是他们·直接的流量为1，这样保证每一个点只被使用一次

#include<queue>
#include<cstdio>
#include<cstring>
#include<iostream>
#include<algorithm>
#define N 2000001
#define inf 9999999
using namespace std;
queue<int>q;
;
int to[N],cap[N],cnt[N],lev[N],head[N],nextt[N];
int read()
{
    ,f=; char ch=getchar();
    ;ch=getchar();}
    +ch-',ch=getchar();
    return x*f;
}
int add(int x,int y,int z)
{
    tot++;to[tot]=y;cap[tot]=z;nextt[tot]=head[x];head[x]=tot;
    tot++;to[tot]=x;cap[tot]=,nextt[tot]=head[y];head[y]=tot;
}
inline bool bfs()
{
    while(!q.empty()) q.pop();
    for(int i=s;i<=e;i++)
    {
        lev[i]=-;
        cnt[i]=head[i];
    }
    q.push(s),lev[s]=;
    while(!q.empty())
    {
        int x=q.front();q.pop();
        for(int i=head[x];i;i=nextt[i])
        {
            int t=to[i];
            &&lev[t]==-)
            {
                lev[t]=lev[x]+;
                q.push(t);
                if(t==e) return true;
            }
        }
    }
    return false;
}
int dinic(int x,int flow)
{
    if(x==e) return flow;
    ;
    for(int &i=cnt[x];i;i=nextt[i])
    {
        int t=to[i];
        &&lev[t]>lev[x])
        {
            delta=dinic(t,min(cap[i],flow-rest));
            if(delta)
            {
                cap[i]-=delta;
                cap[i^]+=delta;
                rest+=delta;
                if(rest==flow) break;
            }
        }
    }
    ;
    return rest;
}
int main()
{
    int n1=read(),n2=read(),n3=read();
    e=n1*+n2+n3+;
    m1=read();
    ;i<=m1;i++)
    {
        x=read(),y=read();
        add(n1*+y,x,);
    }
    m2=read();
    ;i<=m2;i++)
    {
        x=read(),y=read();
        add(x+n1,y+n1*+n2,);
    }
    ;i<=n1;i++)
     add(i,n1+i,);
    ;i<=n2;i++)
     add(s,n1*+i,);
    ;i<=n3;i++)
     add(n1*+n2+i,e,);
    while(bfs())
        ans+=dinic(s,inf);
    printf("%d",ans);
    ;
}