hihocoder网络流一·Ford-Fulkerson算法

网络流一·Ford-Fulkerson算法

时间限制:10000ms

单点时限:1000ms

内存限制:256MB

描述

小Hi和小Ho住在P市，P市是一个很大很大的城市，所以也面临着一个大城市都会遇到的问题：交通拥挤。

小Ho：每到周末回家感觉堵车都是一种煎熬啊。

小Hi：平时交通也还好，只是一到上下班的高峰期就会比较拥挤。

小Ho：要是能够限制一下车的数量就好了，不知道有没有办法可以知道交通系统的最大承受车流量，这样就可以限制到一个可以一直很顺畅的数量了。

小Hi：理论上是有算法的啦。早在1955年，T.E.哈里斯就提出在一个给定的网络上寻求两点间最大运输量的问题。并且由此产生了一个新的图论模型：网络流。

小Ho：那具体是啥？

小Hi：用数学的语言描述就是给定一个有向图G=(V,E)，其中每一条边(u,v)均有一个非负数的容量值，记为c(u,v)≥0。同时在图中有两个特殊的顶点，源点S和汇点T。

举个例子：

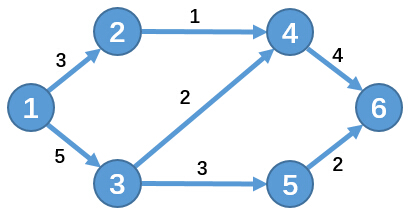
其中节点1为源点S，节点6为汇点T。

我们要求从源点S到汇点T的最大可行流量，这个问题也被称为最大流问题。

在这个例子中最大流量为5，分别为：1→2→4→6，流量为1；1→3→4→6，流量为2；1→3→5→6，流量为2。

小Ho：看上去好像挺有意思的，你让我先想想。

提示：Ford-Fulkerson算法

输入

第1行：2个正整数N,M。2≤N≤500，1≤M≤20,000。

第2..M+1行：每行3个整数u,v,c(u,v)，表示一条边(u,v)及其容量c(u,v)。1≤u,v≤N，0≤c(u,v)≤100。

给定的图中默认源点为1，汇点为N。可能有重复的边。

输出

第1行：1个整数，表示给定图G的最大流。

样例输入

6 7
1 2 3
1 3 5
2 4 1
3 4 2
3 5 3
4 6 4
5 6 2

样例输出

5
分析：最大流关键是求增广路，邻接表存边，便于修改；
代码：

#include <iostream>
#include <cstdio>
#include <cstdlib>
#include <cmath>
#include <algorithm>
#include <climits>
#include <cstring>
#include <string>
#include <set>
#include <map>
#include <queue>
#include <stack>
#include <vector>
#include <list>
#define rep(i,m,n) for(i=m;i<=n;i++)
#define rsp(it,s) for(set<int>::iterator it=s.begin();it!=s.end();it++)
#define mod 1000000007
#define inf 0x3f3f3f3f
#define vi vector<int>
#define pb push_back
#define mp make_pair
#define fi first
#define se second
#define ll long long
#define pi acos(-1.0)
#define pii pair<int,int>
#define Lson L, mid, rt<<1
#define Rson mid+1, R, rt<<1|1
const int maxn=5e2+;
using namespace std;
ll gcd(ll p,ll q){return q==?p:gcd(q,p%q);}
ll qpow(ll p,ll q){ll f=;while(q){if(q&)f=f*p;p=p*p;q>>=;}return f;}
int n,m,k,t,h[maxn],tot,p[maxn],a[maxn],v[maxn][maxn],ans;
struct node
{
    int fr,to,nxt,cap,flow;
}e[<<];
void add(int x,int y,int z)
{
    e[tot].fr=x;
    e[tot].to=y;
    e[tot].nxt=h[x];
    e[tot].cap=z;
    h[x]=tot++;
    e[tot].fr=y;
    e[tot].to=x;
    e[tot].nxt=h[y];
    h[y]=tot++;
}
void max_flow(int s,int t)
{
    ans=;
    while()
    {
        memset(a,,sizeof a);
        queue<int>q;
        q.push(s);a[s]=inf;
        while(!q.empty())
        {
            int x=q.front();
            q.pop();
            for(int i=h[x];i!=-;i=e[i].nxt)
            {
                int to=e[i].to,cap=e[i].cap,flow=e[i].flow;
                if(!a[to]&&cap>flow)
                {
                    p[to]=i;
                    a[to]=min(a[x],cap-flow);
                    q.push(to);
                }
            }
            if(a[t])break;
        }
        if(!a[t])break;
        for(int now=t;now!=s;now=e[p[now]].fr)
        {
            e[p[now]].flow+=a[t];
            e[p[now]^].flow-=a[t];
        }
        ans+=a[t];
    }
}
int main()
{
    int i,j;
    scanf("%d%d",&n,&m);
    memset(h,-,sizeof h);
    while(m--)
    {
        int b,c,d;
        scanf("%d%d%d",&b,&c,&d);
        v[b][c]+=d;
    }
    rep(i,,n)rep(j,,n)if(v[i][j])add(i,j,v[i][j]);
    max_flow(,n);
    printf("%d\n",ans);
    //system("Pause");
    return ;
}

dicnic优化：

#include <iostream>
#include <cstdio>
#include <cstdlib>
#include <cmath>
#include <algorithm>
#include <climits>
#include <cstring>
#include <string>
#include <set>
#include <map>
#include <queue>
#include <stack>
#include <vector>
#include <list>
#define rep(i,m,n) for(i=m;i<=n;i++)
#define rsp(it,s) for(set<int>::iterator it=s.begin();it!=s.end();it++)
#define mod 1000000007
#define inf 0x3f3f3f3f
#define vi vector<int>
#define pb push_back
#define mp make_pair
#define fi first
#define se second
#define ll long long
#define pi acos(-1.0)
#define pii pair<int,int>
#define Lson L, mid, rt<<1
#define Rson mid+1, R, rt<<1|1
const int maxn=5e2+;
using namespace std;
ll gcd(ll p,ll q){return q==?p:gcd(q,p%q);}
ll qpow(ll p,ll q){ll f=;while(q){if(q&)f=f*p;p=p*p;q>>=;}return f;}
int n,m,k,t,h[maxn],tot,vis[maxn],s,cur[maxn];
struct node
{
    int fr,to,nxt,cap,flow;
}e[<<];
void add(int x,int y,int z)
{
    e[tot].fr=x;
    e[tot].to=y;
    e[tot].nxt=h[x];
    e[tot].cap=z;
    h[x]=tot++;
    e[tot].fr=y;
    e[tot].to=x;
    e[tot].nxt=h[y];
    h[y]=tot++;
}
bool bfs()
{
    memset(vis,,sizeof vis);
    queue<int>p;
    p.push(s);
    vis[s]=;
    while(!p.empty())
    {
        int x=p.front();p.pop();
        for(int i=h[x];i!=-;i=e[i].nxt)
        {
            int to=e[i].to,cap=e[i].cap,flow=e[i].flow;
            if(!vis[to]&&cap>flow)
            {
                vis[to]=vis[x]+;
                p.push(to);
            }
        }
    }
    return vis[t];
}
int dfs(int x,int a)
{
    if(x==t||a==)return a;
    int ans=,j;
    for(int&i=cur[x];i!=-;i=e[i].nxt)
    {
        int to=e[i].to,cap=e[i].cap,flow=e[i].flow;
        if(vis[to]==vis[x]+&&(j=dfs(to,min(a,cap-flow)))>)
        {
            e[i].flow+=j;
            e[i^].flow-=j;
            ans+=j;
            a-=j;
            if(a==)break;
        }
    }
    return ans;
}
int max_flow(int s,int t)
{
    int flow=,i;
    while(bfs())
    {
        rep(i,,n)cur[i]=h[i];
        flow+=dfs(s,inf);
    }
    return flow;
}
int main()
{
    int i,j;
    memset(h,-,sizeof h);
    scanf("%d%d",&n,&m);
    while(m--)
    {
        int a,b,c;
        scanf("%d%d%d",&a,&b,&c);
        add(a,b,c);
    }
    s=,t=n;
    printf("%d\n",max_flow(s,t));
    //system("Pause");
    return ;
}