Lorenzo Von Matterhorn

Lorenzo Von Matterhorn

Barney lives in NYC. NYC has infinite number of intersections numbered with positive integers starting from 1. There exists a bidirectional road between intersections i and 2i and another road between i and 2i + 1 for every positive integer i. You can clearly see that there exists a unique shortest path between any two intersections.

Initially anyone can pass any road for free. But since SlapsGiving is ahead of us, there will q consecutive events happen soon. There are two types of events:

1. Government makes a new rule. A rule can be denoted by integers v, u and w. As the result of this action, the passing fee of all roads on the shortest path from u to v increases by w dollars.

2. Barney starts moving from some intersection v and goes to intersection u where there's a girl he wants to cuddle (using his fake name Lorenzo Von Matterhorn). He always uses the shortest path (visiting minimum number of intersections or roads) between two intersections.

Government needs your calculations. For each time Barney goes to cuddle a girl, you need to tell the government how much money he should pay (sum of passing fee of all roads he passes).

Input

The first line of input contains a single integer q (1 ≤ q ≤ 1 000).

The next q lines contain the information about the events in chronological order. Each event is described in form 1 v u w if it's an event when government makes a new rule about increasing the passing fee of all roads on the shortest path from u to v by w dollars, or in form 2 v u if it's an event when Barnie goes to cuddle from the intersection v to the intersection u.

1 ≤ v, u ≤ 10¹⁸, v ≠ u, 1 ≤ w ≤ 10⁹ states for every description line.

Output

For each event of second type print the sum of passing fee of all roads Barney passes in this event, in one line. Print the answers in chronological order of corresponding events.

Example

Input

7
1 3 4 30
1 4 1 2
1 3 6 8
2 4 3
1 6 1 40
2 3 7
2 2 4

Output

94
0
32

Note

In the example testcase:

Here are the intersections used:

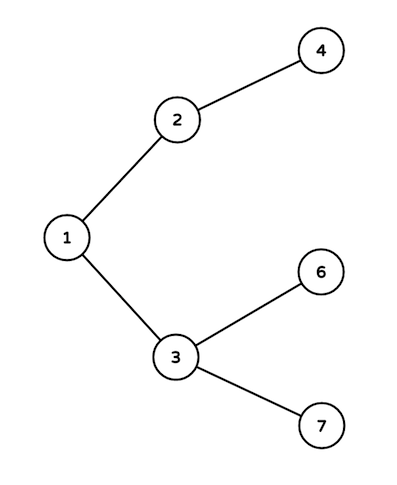
1. Intersections on the path are 3, 1, 2 and 4.
2. Intersections on the path are 4, 2 and 1.
3. Intersections on the path are only 3 and 6.
4. Intersections on the path are 4, 2, 1 and 3. Passing fee of roads on the path are 32, 32 and 30 in order. So answer equals to 32 + 32 + 30 = 94.
5. Intersections on the path are 6, 3 and 1.
6. Intersections on the path are 3 and 7. Passing fee of the road between them is 0.
7. Intersections on the path are 2 and 4. Passing fee of the road between them is 32 (increased by 30 in the first event and by 2 in the second).

分析：这种二叉树两节点的最短路径是先找到最近公共祖先(LCA)，然后就是分别从当前节点到祖先的路径；

代码：

#include <iostream>
#include <cstdio>
#include <cstdlib>
#include <cmath>
#include <algorithm>
#include <climits>
#include <cstring>
#include <string>
#include <set>
#include <map>
#include <queue>
#include <stack>
#include <vector>
#include <list>
#include <ext/rope>
#define rep(i,m,n) for(i=m;i<=n;i++)
#define rsp(it,s) for(set<int>::iterator it=s.begin();it!=s.end();it++)
#define vi vector<int>
#define pii pair<int,int>
#define mod 1000000007
#define inf 0x3f3f3f3f
#define pb push_back
#define mp make_pair
#define fi first
#define se second
#define ll long long
#define pi acos(-1.0)
const int maxn=1e5+;
const int dis[][]={{,},{-,},{,-},{,}};
using namespace std;
using namespace __gnu_cxx;
ll gcd(ll p,ll q){return q==?p:gcd(q,p%q);}
ll qpow(ll p,ll q){ll f=;while(q){if(q&)f=f*p;p=p*p;q>>=;}return f;}
int n,m;
map<ll,ll>p;
ll a[],fa,fb,ans;
int main()
{
    int i,j,k,t;
    scanf("%d",&t);
    while(t--)
    {
        scanf("%lld",&a[]);
        if(a[]==)
        {
            rep(i,,)scanf("%lld",&a[i]);
            fa=a[],fb=a[];
            while(fa!=fb)
            {
                if(fa<fb)p[fb]+=a[],fb>>=;
                else p[fa]+=a[],fa>>=;
            }
        }
        else
        {
            rep(i,,)scanf("%lld",&a[i]);
            ans=0LL;
            fa=a[],fb=a[];
            while(fa!=fb)
            {
                if(fa<fb)ans+=p[fb],fb>>=;
                else ans+=p[fa],fa>>=;
            }
            printf("%lld\n",ans);
        }
    }
    //system ("pause");
    return ;
}