UVA 11551 Experienced Endeavour

矩阵快速幂。

题意事实上已经告诉我们这是一个矩阵乘法的运算过程。

构造矩阵：把xi列的bij都标为1.

例如样例二：

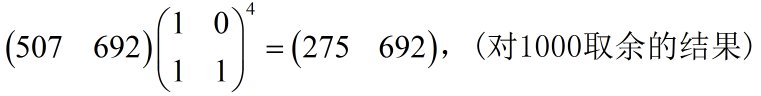
#include<cstdio>
#include<cstring>
#include<cmath>
#include<vector>
#include<algorithm>
using namespace std;

long long const MOD = ;
int n, m;
long long a[ + ];

struct Matrix
{
    long long A[ + ][ + ];
    int R, C;
    Matrix operator*(Matrix b);
};

Matrix X, Y, Z;

Matrix Matrix::operator*(Matrix b)
{
    Matrix c;
    memset(c.A, , sizeof(c.A));
    int i, j, k;
    for (i = ; i <= R; i++)
    for (j = ; j <= b.C; j++)
    for (k = ; k <= C; k++)
        c.A[i][j] = (c.A[i][j] + (A[i][k] * b.A[k][j]) % MOD) % MOD;
    c.R = R; c.C = b.C;
    return c;
}

void init()
{
    memset(X.A, , sizeof X.A);
    memset(Y.A, , sizeof Y.A);
    memset(Z.A, , sizeof Z.A);

    Y.R = n; Y.C = n;
    for (int i = ; i <= n; i++) Y.A[i][i] = ;

    X.R = n; X.C = n;
    for (int j = ; j <= n; j++)
    {
        int xi; scanf("%d", &xi);
        for (int i = ; i <= xi; i++)
        {
            int num; scanf("%d", &num); num++;
            X.A[num][j] = ;
        }
    }

    Z.R = ; Z.C = n;
    for (int i = ; i <= n; i++) Z.A[][i] = a[i];

}

void read()
{
    scanf("%d%d", &n, &m);
    for (int i = ; i <= n; i++)
    {
        scanf("%lld", &a[i]);
        a[i] = a[i] % MOD;
    }
}

void work()
{
    while (m)
    {
        if (m %  == ) Y = Y*X;
        m = m >> ;
        X = X*X;
    }
    Z = Z*Y;

    for (int i = ; i <= n; i++)
    {
        printf("%lld", Z.A[][i]);
        if (i<n) printf(" ");
        else printf("\n");
    }
}

int main()
{
    int T;
    scanf("%d", &T);
    while (T--)
    {
        read();
        init();
        work();
    }
    return ;
}