杨辉三角形II(Pascal's Triangle II)

杨辉三角形II(Pascal's Triangle II)

问题

给出一个索引k，返回杨辉三角形的第k行。

例如，给出k = 3，返回[1, 3, 3, 1]

注意：

你可以优化你的算法使之只使用O(k)的额外空间吗？

初始思路

首先来复习复习杨辉三角形的性质（来自wiki）：

1. 杨辉三角以正整数构成，数字左右对称，每行由1开始逐渐变大，然后变小，回到1。
2. 第行的数字个数为个。
3. 第行的第个数字为组合数。
4. 第行数字和为。
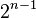5. 除每行最左侧与最右侧的数字以外，每个数字等于它的左上方与右上方两个数字之和（也就是说，第行第个数字等于第行的第个数字与第个数字的和）。这是因为有组合恒等式：。可用此性质写出整个杨辉三角形。

看到第2条和5条是不是发现和 [LeetCode 120] - 三角形(Triangle) 中的最终算法有点像？没错，这里可以使用类似的方法得出杨辉三角形中第k行的数据，而且更简单：

• 第1列和最后1列的数字永远为1
• 其他列如性质5所述，为上一行纵坐标j-1和纵坐标j的点之和

最终得出的只是用O(k)额外空间的代码如下：

 getRow

1 class Solution {
 2     public:
 3         std::vector<int> getRow(int rowIndex)
 4         {
 5             std::vector<int> columnInfo(rowIndex + 1);
 6
 7             columnInfo[0] = 1;
 8
 9             if(rowIndex == 0)
10             {
11                 return columnInfo;
12             }
13
14             columnInfo[1] = 1;
15
16             for(int i = 1; i < rowIndex + 1; ++i)
17             {
18                 for(int j = i; j > 0; --j)
19                 {
20                     if(j == 0 || j == i)
21                     {
22                         columnInfo[j] = 1;
23                     }
24                     else
25                     {
26                         columnInfo[j] = columnInfo[j - 1] + columnInfo[j];
27                     }
28                 }
29             }
30
31             return columnInfo;
32         }
33 };

顺利通过Judge Small和Judge Large。

题外

根据杨辉三角形的性质3，我们也可以直接计算某行所有数的值。由于对称性，实际只需要计算前一半的列并将结果拷贝到后一半列即可。但是这种方法的问题是需要计算很大的阶乘，当行数达到一定大小时不做特殊处理就会溢出了。以下是一个示例，没做特殊处理，只是用int64_t保存中间结果。当输入为21时就会溢出了：

 阶乘－有缺陷

1 class SolutionV2 {
 2     public:
 3         std::vector<int> getRow(int rowIndex)
 4         {
 5             std::vector<int> columnInfo(rowIndex + 1);
 6
 7             nFactorial_ = 1;
 8
 9             for(int i = 1; i <= rowIndex; ++i)
10             {
11                 nFactorial_ *= i;
12             }
13
14             columnInfo[0] = 1;
15             columnInfo[rowIndex] = 1;
16
17             for(int i = 1; i <= rowIndex / 2; ++i)
18             {
19                 columnInfo[i] = CaculateCombination(rowIndex, i);
20             }
21
22             int left = 1;
23             int right = rowIndex - 1;
24
25             while(left < right)
26             {
27                 columnInfo[right] = columnInfo[left];
28                 ++left;
29                 --right;
30             }
31
32
33             return columnInfo;
34         }
35
36     private:
37         int64_t CaculateCombination(int n, int k)
38         {
39             int64_t kFactorial = 1;
40             int64_t restFactorial = 1;
41
42             for(int i = 1; i <= k; ++i)
43             {
44                 kFactorial *= i;
45             }
46
47             for(int i = 1; i <= n - k; ++i)
48             {
49                 restFactorial *= i;
50             }
51
52             return nFactorial_ / (kFactorial * restFactorial);
53         }
54
55         int64_t nFactorial_;
56     };

 

 

分类: LeetCode

标签: c++, leetcode, 算法