kernel function

下面这张图位于第一、二象限内。我们关注红色的门，以及“北京四合院”这几个字下面的紫色的字母。我们把红色的门上的点看成是“+”数据，紫色字母上的点看成是“-”数据，它们的横、纵坐标是两个特征。显然，在这个二维空间内，“+”“-”两类数据不是线性可分的。

我们现在考虑核函数，即“内积平方”。
这里面是二维空间中的两个点。

这个核函数对应着一个二维空间到三维空间的映射，它的表达式是：

可以验证，

在P这个映射下，原来二维空间中的图在三维空间中的像是这个样子：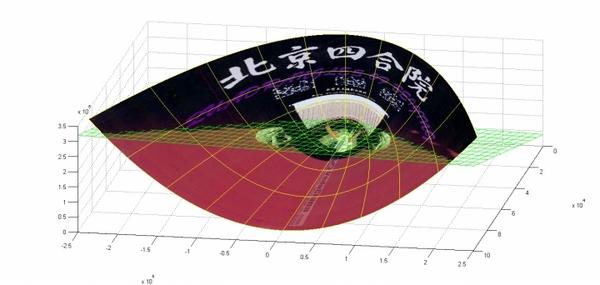
（前后轴为x轴，左右轴为y轴，上下轴为z轴）
注意到绿色的平面可以完美地分割红色和紫色，也就是说，两类数据在三维空间中变成线性可分的了。
而三维中的这个判决边界，再映射回二维空间中是这样的：
这是一条双曲线，它不是线性的。

================================================

如上面的例子所说，核函数的作用就是隐含着一个从低维空间到高维空间的映射，而这个映射可以把低维空间中线性不可分的两类点变成线性可分的。

当然，我举的这个具体例子强烈地依赖于数据在原始空间中的位置。
事实中使用的核函数往往比这个例子复杂得多。它们对应的映射并不一定能够显式地表达出来；它们映射到的高维空间的维数也比我举的例子（三维）高得多，甚至是无穷维的。这样，就可以期待原来并不线性可分的两类点变成线性可分的了。

================================================

在机器学习中常用的核函数，一般有这么几类，也就是LibSVM中自带的这几类：
1) 线性：
2) 多项式：
3) Radial basis function：
4) Sigmoid：

我举的例子是多项式核函数中的情况。

在实用中，很多使用者都是盲目地试验各种核函数，并扫描其中的参数，选择效果最好的。至于什么样的核函数适用于什么样的问题，大多数人都不懂。很不幸，我也属于这大多数人，所以如果有人对这个问题有理论性的理解，还请指教。

================================================

核函数要满足的条件称为Mercer's condition。
由于我以应用SVM为主，对它的理论并不很了解，就不阐述什么了。
使用SVM的很多人甚至都不知道这个条件，也不关心它；有些不满足该条件的函数也被拿来当核函数用。