[CSP-S模拟测试]:辣鸡(ljh) （暴力）

题目描述

辣鸡$ljh\ NOI$之后就退役了，然后就滚去学文化课了。
然而在上化学课的时候，数学和化学都不好的$ljh$却被一道简单题难住了，受到了大佬的嘲笑。
题目描述是这样的：
在一个二维平面上有一层水分子，请问形成了多少个氢键？
这个二维平面可以看做一个类似棋盘的东西，每个格子可以容纳一个水分子，左下角的格子为$(0,0)$，这个格子右边的格子为$(1,0)$，上方格子为$(0,1)$，以此类推。
辣鸡$ljh$当然不会做了，所以他来求助$JeremyGou$，$JeremyGou$一眼就看穿了真相，并想用这道题来考一考正在做$NOIP$模拟赛的你。
注：在本题中，我们认为一个水分子能与和它曼哈顿距离为$2$且直线距离小于$2$的其他格子形成氢键。

---

输入格式

一个整数$n$。
接下来$n$行，每行给出四个整数$x_1,y_1,x_2,y_2$。
表示以$(x_1,y_1)$为左下角，$(x_2,y_2)$为右上角的矩形中每个格子都有一个水分子。
给出的所有矩形没有交集。

---

输出格式

一个整数，表示氢键的数量。

---

样例

样例输入1：

3
0 0 0 0
0 1 1 2
2 2 2 3

样例输出1：

5

样例输入2：

10
1 8 8 9
0 3 10 7
0 0 7 0
0 2 9 2
4 10 8 10
10 0 10 2
0 10 0 10
8 0 9 1
0 8 0 9
9 8 10 8

样例输出2：

157

---

数据范围与提示

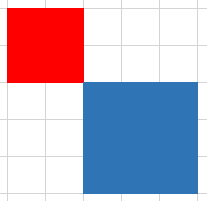
样例$1$解释：

左图为水分子的排布，右图中的绿色线条表示氢键。

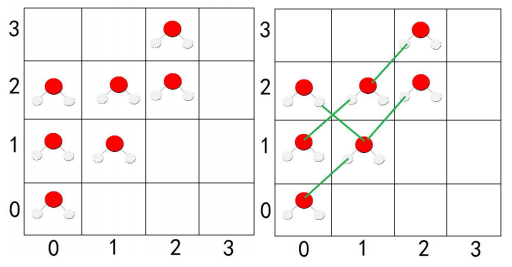
$N\leqslant {10}^5$。

$x\leqslant {10}^9$。

$y\leqslant {10}^9$。

自己画的样例$2\downarrow$：

---

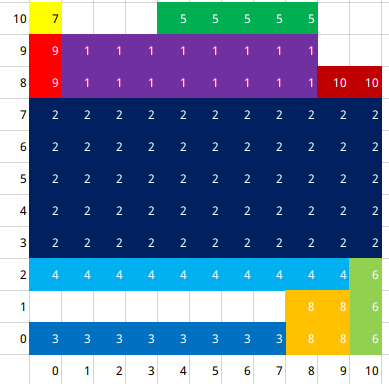
题解

$15\%$算法：

开一个临接矩阵，存一下，在里面$\Theta(\max(x_{2_i},y_{2_i})^2)$跑一遍就好了。

$35\%$算法：

$\Theta(n^2)$枚举每对矩形，统计它们之间形成的贡献，在加上它们内部的贡献即可。

$65\%$算法：

$\Theta(n)$枚举每个矩形，输出它们的内部贡献，即$(x_2-x_1)\times(y_2-y_1)\times 2$，是不是很震惊？！？！

$100\%$算法：

先按$x_1$的大小排个序，然后再进行$\Theta(n^2)$进行枚举，如果$x_j-x_i>1$则$break$。

统计答案的时候分4种情况：

　　$\alpha.$每个矩形自己内部的贡献。

　　$\beta.$两个矩形左右相接。

　　

if(min(e[i].x2,e[j].x2)-max(e[i].x1,e[j].x1)>=0)
{
	if(e[i].y2==e[j].y1-1)
	{
		ans+=(min(e[i].x2,e[j].x2)-max(e[i].x1,e[j].x1))<<1;
		if(e[i].x1!=e[j].x1)ans++;
		if(e[i].x2!=e[j].x2)ans++;
	}
	if(e[j].y2==e[i].y1-1)
	{
		ans+=(min(e[i].x2,e[j].x2)-max(e[i].x1,e[j].x1))<<1;
		if(e[i].x1!=e[j].x1)ans++;
		if(e[i].x2!=e[j].x2)ans++;
	}
}

　　$\chi.$两个矩形上下相接。

　　

if(min(e[i].y2,e[j].y2)-max(e[i].y1,e[j].y1)>=0)
{
	if(e[i].x2==e[j].x1-1)
	{
		ans+=(min(e[i].y2,e[j].y2)-max(e[i].y1,e[j].y1))<<1;
		if(e[i].y1!=e[j].y1)ans++;
		if(e[i].y2!=e[j].y2)ans++;
	}
	if(e[j].x2==e[i].x1-1)
	{
		ans+=(min(e[i].y2,e[j].y2)-max(e[i].y1,e[j].y1))<<1;
		if(e[i].y1!=e[j].y1)ans++;
		if(e[i].y2!=e[j].y2)ans++;
	}
}

　　$\delta.$两个矩形对角

　　

if(e[i].x2==e[j].x1-1&&(e[i].y2==e[j].y1-1||e[i].y1==e[j].y2+1))ans++;

这就是正解？！？！

没错，至少出题人这么说的；而对于这道题，出题人就是老大……

---

代码时刻

#include<bits/stdc++.h>
using namespace std;
struct rec
{
	int x1;
	int y1;
	int x2;
	int y2;
}e[100001];
long long ans;
bool cmp1(rec a,rec b){return a.x1<b.x1;}
int main()
{
	int n;
	scanf("%d",&n);
	for(register int i=1;i<=n;i++)
	{
		scanf("%d%d%d%d",&e[i].x1,&e[i].y1,&e[i].x2,&e[i].y2);
		ans+=1LL*(e[i].x2-e[i].x1)*(e[i].y2-e[i].y1);
	}
	ans<<=1;
	sort(e+1,e+n+1,cmp1);
	for(register int i=1;i<n;i++)
		for(register int j=i+1;j<=n;j++)
		{
			if(e[j].x1-e[i].x2>1)break;
			if(min(e[i].x2,e[j].x2)-max(e[i].x1,e[j].x1)>=0)
			{
				if(e[i].y2==e[j].y1-1)
				{
					ans+=(min(e[i].x2,e[j].x2)-max(e[i].x1,e[j].x1))<<1;
					if(e[i].x1!=e[j].x1)ans++;
					if(e[i].x2!=e[j].x2)ans++;
				}
				if(e[j].y2==e[i].y1-1)
				{
					ans+=(min(e[i].x2,e[j].x2)-max(e[i].x1,e[j].x1))<<1;
					if(e[i].x1!=e[j].x1)ans++;
					if(e[i].x2!=e[j].x2)ans++;
				}
			}
			if(min(e[i].y2,e[j].y2)-max(e[i].y1,e[j].y1)>=0)
			{
				if(e[i].x2==e[j].x1-1)
				{
					ans+=(min(e[i].y2,e[j].y2)-max(e[i].y1,e[j].y1))<<1;
					if(e[i].y1!=e[j].y1)ans++;
					if(e[i].y2!=e[j].y2)ans++;
				}
				if(e[j].x2==e[i].x1-1)
				{
					ans+=(min(e[i].y2,e[j].y2)-max(e[i].y1,e[j].y1))<<1;
					if(e[i].y1!=e[j].y1)ans++;
					if(e[i].y2!=e[j].y2)ans++;
				}
			}
			if(e[i].x2==e[j].x1-1&&(e[i].y2==e[j].y1-1||e[i].y1==e[j].y2+1))ans++;
		}
	printf("%lld",ans);
	return 0;
}

---

rp++