核磁共振成像学习笔记——从FID信号到K空间

在理想磁场环境下（没有不存在场不均匀性），对于一个没有梯度场的方块。





此时，RF pulse的两路正交信号（相位差为90°）对此方块进行激发，然后收取信号，我们可以得到由此方块产生的FID信号。





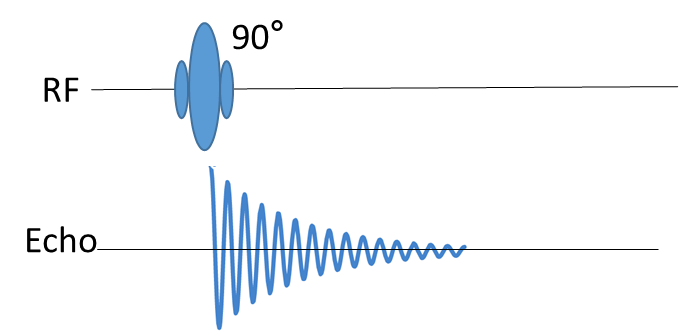
设此信号为\(S(t)\)，则此信号由\(S_c(t)\)与\(S_s(t)\)组成，分别组成\(S(t)\)的实部与虚部。

\[\left\{
\begin{aligned}
S_c(t)=M_{xy}e^{-t/T_2}\cos({\omega}t)\\
S_s(t)=M_{xy}e^{-t/T_2}\sin({\omega}t)
\end{aligned}
\right.
\]

这是我们的接受线圈接收到的两组正交信号。

再利用欧拉公式

\[\left\{
\begin{aligned}
\cos({\omega}t)=\frac{e^{i{\omega}t}+e^{-{i{\omega}t}}}{2}\\
\sin({\omega}t)=\frac{e^{i{\omega}t}-e^{-{i{\omega}t}}}{2i}
\end{aligned}
\right.
\]

使

\[ S(t)=S_c(t)+iS_s(t)
\]

则

\[ S(t)=M_{xy}*e^{-t/T_2}*e^{-i{\omega}t}
\]

此时，我们忽略衰减项\(e^{-t/T_2}\)，则

\[ S(t)=M_{xy}*e^{-i{\omega}t}
\]

这是我们对单个方块进行激发的结果，那么此时，引入梯度磁场进行空间定位。





根据拉莫尔进动(Larmor precession)

\[ \omega={\gamma}B
\]

Phase encoding gradient和frequency encoding gradient的出现会使得这个方块内部的每个位置的进动频率\(\omega\)发生变化。但需要注意Phase encoding gradient和frequency encoding gradient是不能够同时开启的(SE序列中)。然后，我们看自旋回波序列(SE)。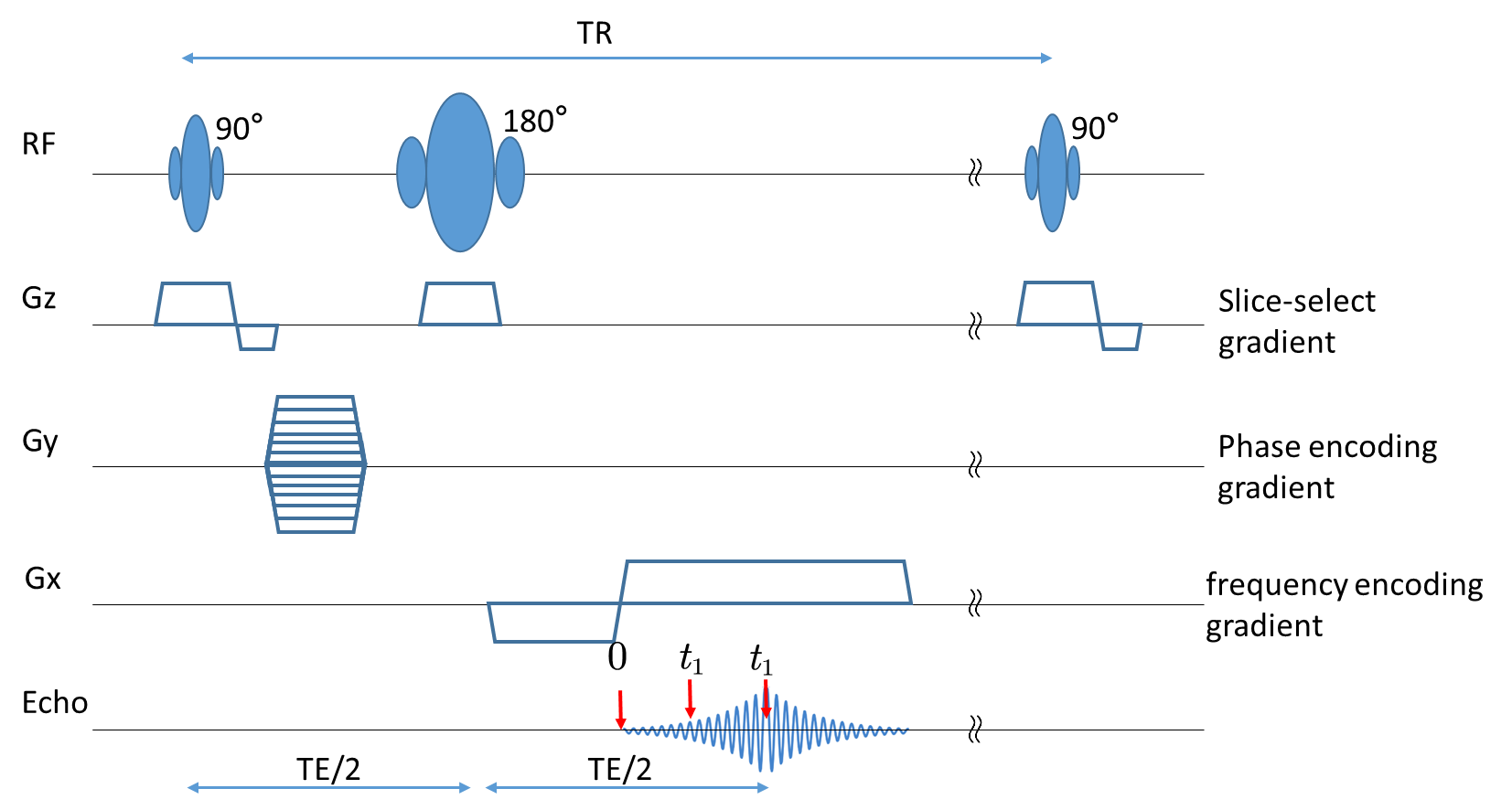

在接收信号前，分别开启了一段Phase encoding gradient和frequency encoding gradient。在接收信号的时候，frequency encoding gradient全程保持开启。

先进行公式推导，\(S(t)\)即为上文理想方块条件下推导得出的，我们将\(M_{xy}\)设定为\(\rho(x,y)\)表示方块中每个位置在加权设定后的信号强度，则

\[ S(t)=\iint{\rho(x,y)e^{-i\phi(x,y,t)}}dxdy
\]

其中

\[ \phi(x,y,t)={\gamma}\int_{0}^{t}{[G_x(t^{\prime})x+G_y(t)y]}dt^{\prime}
\]

设定\(G_x\)为frequency encoding gradient，\(G_y\)为Phase encoding gradient，和序列图中保持一致，\(0\)至\(t\)为开始采样至实时采样的时间，SE序列图中的\(t_1\)和\(t_2\)为其中的两个\(t\)（这是一个变上限积分）。

令

\[\left\{
\begin{aligned}
k_x=2\pi\int_{0}^{t}{G_x(t^{\prime})}dt^{\prime}\\
k_y=2\pi\int_{0}^{t}{G_y(t)}dt^{\prime}
\end{aligned}
\right.
\]

则

\[ S(t)=\iint{\rho(x,y)e^{-i2\pi[k_xx+k_yy]}}dxdy
\]

即

\[ S(k_x,k_y)=\iint{\rho(x,y)e^{-i2\pi[k_xx+k_yy]}}dxdy
\]

至此，在数学上说明了\(S(t)\)与\(\rho(x,y)\)互为傅里叶变换对。这时，我们将方块分割为一个3*3的方块进行进一步的说明。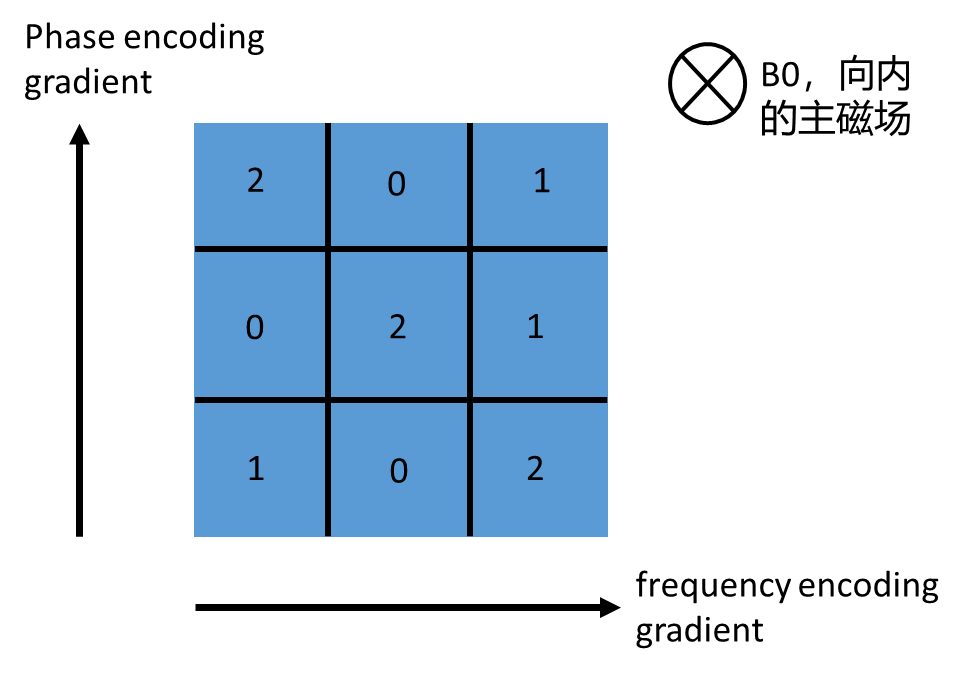

其中的数值为该位置对应的\(\rho(x,y)\)数值。

以\(S_c(t)\)信号为例，其组成的是\(S(t)\)中的实部，在没有进行空间编码前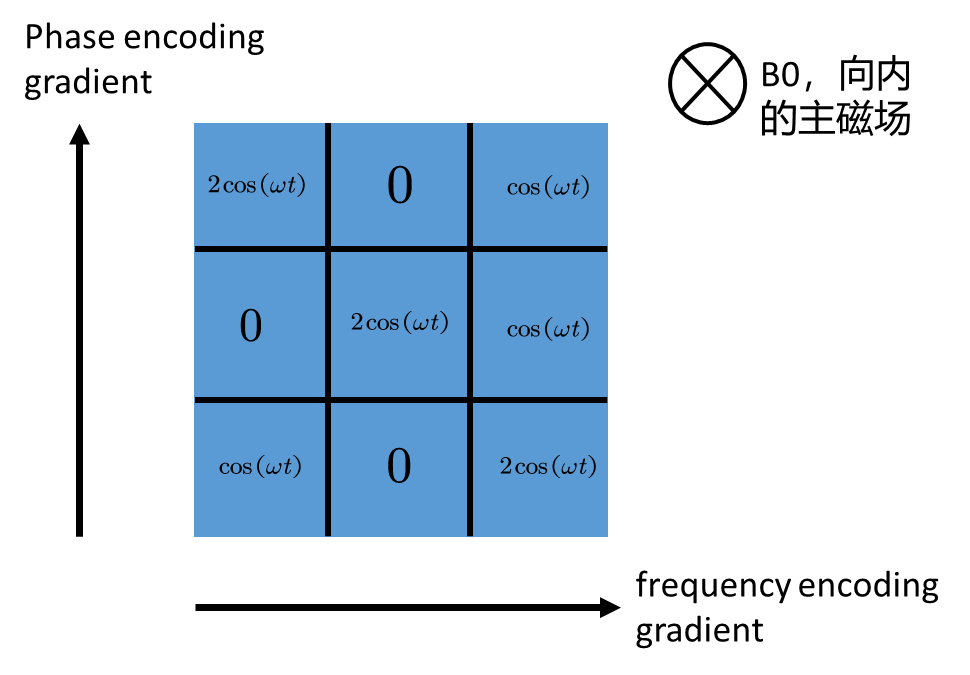

根据SE序列的波形，先是进行了Phase encoding gradient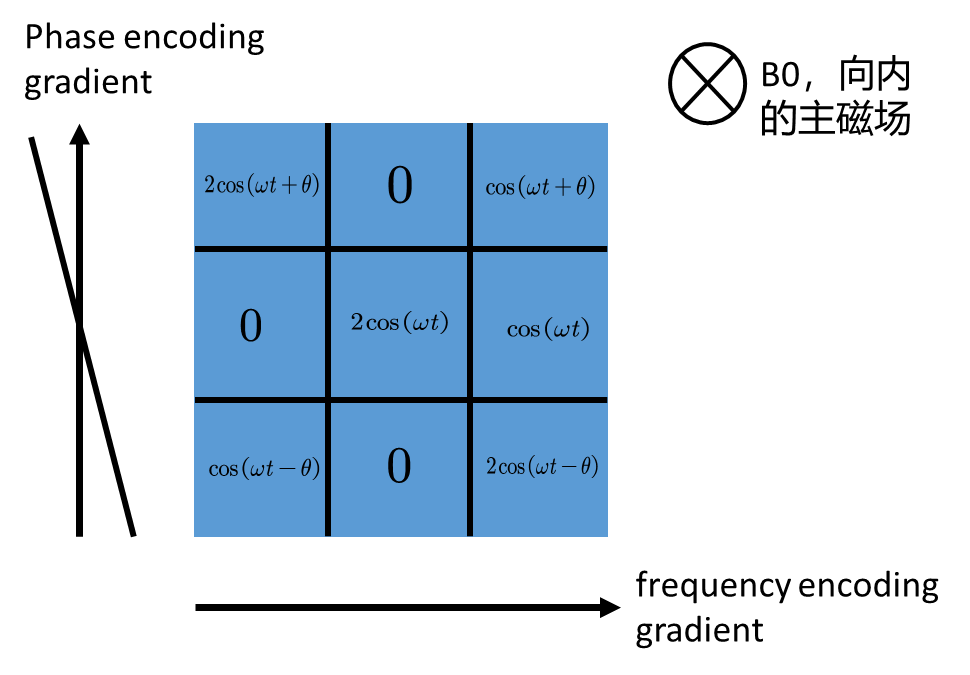

Phase encoding gradient改变的也是\(\omega\)，但作用了一段时间就停止了，相当于把纵向的各个单位以不同的\(\omega\)推了相同的时间，那么他们的相位\(\theta\)就发生了变化。并且，通过改变Phase encoding gradient的斜率，可以使得\(\theta\)的数值发生变化，对于一个3*3的方块，想要进行空间定位就要改变三次Phase encoding gradient斜率。

然后在收取数据的同时，进行frequency encoding gradient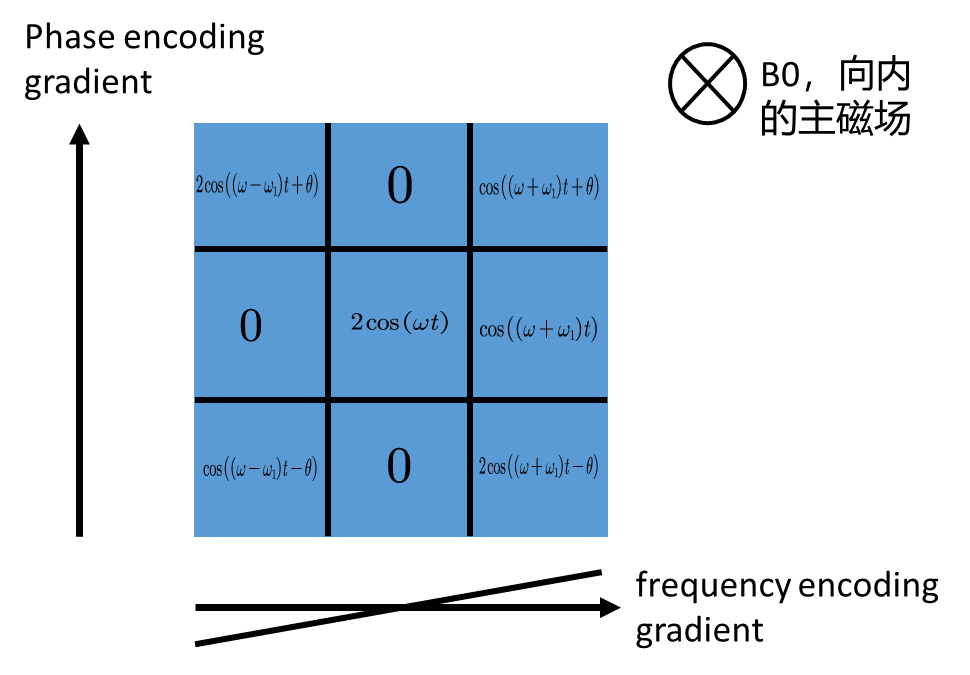

frequency encoding gradient同样改变了\(\omega\)，并且与收取信号同时进行，就此完成了区块的空间定位。通俗的来说，假设这些区块在一个环形的跑道进行赛跑，Phase encoding gradient就相当于在跑步开始之前，将同一个跑道上的每个跑者推到不同的起点上，frequency encoding gradient相当于使得不同跑道上的跑者有不同的跑步速度。

让我们回到公式

\[\left\{
\begin{aligned}
k_x=2\pi\int_{0}^{t}{G_x(t^{\prime})}dt^{\prime}\\
k_y=2\pi\int_{0}^{t}{G_y(t)}dt^{\prime}
\end{aligned}
\right.
\]

这里面的\(k_x\)与\(k_y\)就是位于K空间的\(xy\)坐标（注意\(t\)与\(t^{\prime}\)的区别）。\(G_y(t)\)就是Phase encoding gradient，在SE序列中每次都需要重新变化斜率，需要在y方向将区域分割成多少块，就需要变化多少次斜率，每次变化都需要经过一个\(TR\)。而\(G_x\)则保持不变，并且只需要增加采样点数就可以增加此方向的区块分割，不需要增加采样的时间。故我们使用SE序列进行图像重建的时候，最好将分块更多的方向对应frequency encoding gradient，因为每次Phase encoding gradient都需要消耗一个\(TR\)。这里我截取MRI,The Basics书中的一幅图说明这一点。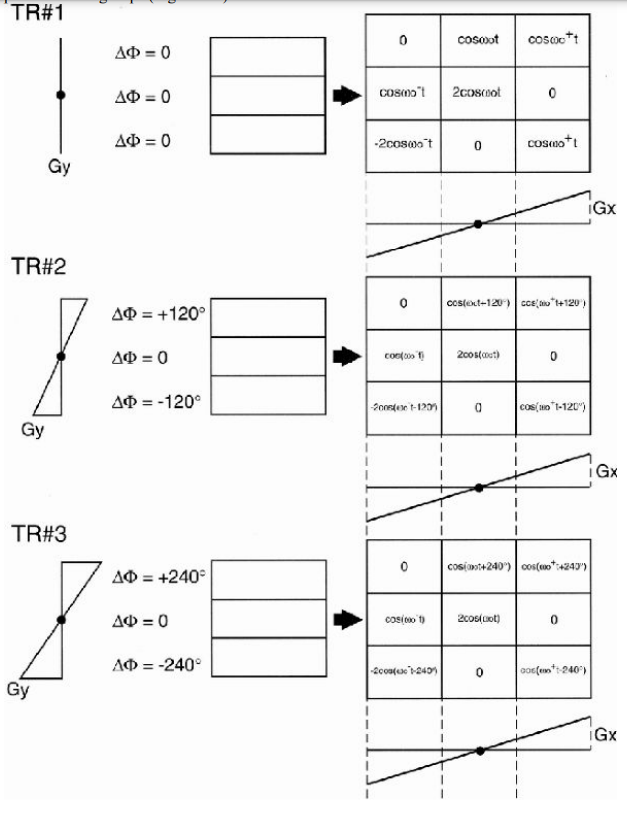

对于一个\(3*3\)的方块，哪边放在frequency encoding gradient都无所谓。但如果是一个\(128*256\)的方块，那么就需要将256的那条边放在frequency encoding gradient上，以减少重建时间。

参考:

[1]MRI From Picture to Proton

[2]MRI, The Basics

[3]MRI磁振影像學 盧家鋒

[4]MRI原理-信号 - lemon lelieven的文章 - 知乎 https://zhuanlan.zhihu.com/p/137255997

[5]【磁共振的K空间】 https://www.bilibili.com/video/BV1ch411e7Yc/?share_source=copy_web&vd_source=0e8c3fe50c67df43ceeb30f63e36eb0d