自然常数e的由来以及计算机为什么是二进制

背景

昨晚我在看一本书，叫《数学极客》，看到第六章《e：不自然的自然数》，这个数最早开始接触应该是高一的时候，那时候问老师，这个数是怎么来的，老实说，和圆周率一样，是一个常数，然后就没有然后了，后面这个问题就随着我的好奇心一起沉睡了，直到昨晚这个尘封许久的问题又一次浮上我的心头，庆幸的是这次我有了打破砂锅问到底的想法和行动。特意写下这篇文章纪念这一次探索之旅。

e是怎么来的？

这个数其实来源于1683年瑞士数学家雅各布·伯努利以及他所研究的复利问题。复利问题是这样的，如果你有a元，存进银行里，银行一年之后付你100%的利息，那么你一年之后能拿到的钱就是：

\[y = a(1 + 1)
\]

但是现在要是银行改变策略了，变成半年付一次利息，并且一次利息为50%，那么一年后你能拿到多少呢？是下面这个数：

\[y = a(1 +\frac{1}{2})^2
\]

其实很明显我们可以看出来，分的份数越多可以拿到的更多，因为下一次结算利息是以上一次发放的本金加上利息作为本金计算出来的。那么自然而然，我们会好奇，要是把一年的时间分成无穷大份，我们一年之后能得到多少？这个计算也简单嘛。就是下面这个式子：

\[y = a\lim_{n\rightarrow+\infty}(1 + \frac{1}{n})^n
\]

我们看这个式子，其实a是常数，也就是我们的原始本金，不需要纳入讨论的范畴，我们关键还是看后面的部分。当n趋于无穷的时候后面这个1+1/n的n次方代表着我们这笔钱能翻几倍。伯努利发现这个数趋近无穷大的时候，这个数会毕竟一个小数，也就是我们熟知的2.718。

这个2.718是怎么算的呢？我们可以把e^x用泰勒公式展开：

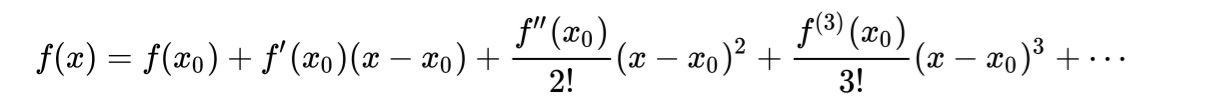
当f(x)是e^x的时候代入进去：

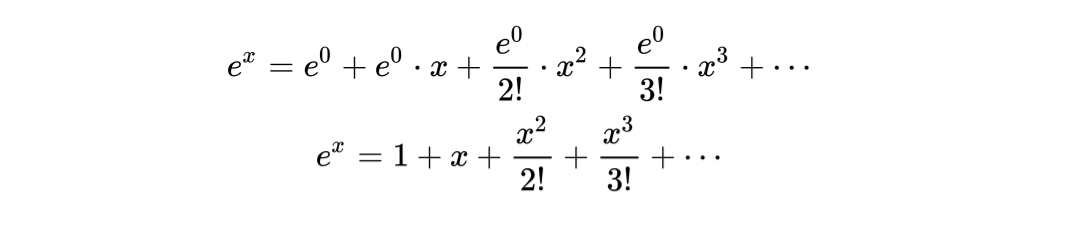
当x是1的时候也就是我们要计算的e的值：

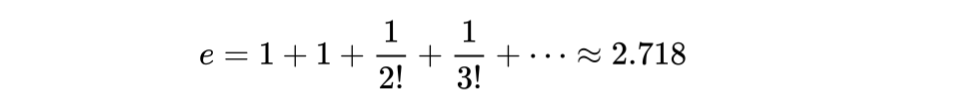
一开始这个数还不叫e，他叫b。后来欧拉出现了，他觉得呀，你这个式子趋近于一个常数，是好事情，但是你一开始的假设他的一年后翻一倍，后面也是基于这个假设，把一年分成若干份，每次发放的利息是若干份之一，这个结论不够一般化，所以把这个东西推广了一下。一年之后的利息总是x。就变成了下面这个式子：

\[a\lim_{n\rightarrow+\infty}(1 + \frac{x}{n})^n
\]

可以看出来，这个式子其实就变成了关于x的函数了，一般在数学上表示一个关于x的函数都是用f(x), 但是这里欧啦用了exp(x)来表示, exp就是指数的意思。也就是：

\[exp(x) = a\lim_{n\rightarrow+\infty}(1 + \frac{x}{n})^n
\]

这个也就是指数函数最开始的定义。到这里就会有人问了，指数不是y=a^x这种形式嘛。其实你这样看，就豁然开朗了:

\[exp(x) = a\lim_{n\rightarrow+\infty}((1 + (\frac{x}{n})^\frac{n}{x})^x
\]

上面这两个式子其实是等价的，就是稍微操作了一下。n除x，在外面又乘x。但是这里你仔细观察

\[\lim_{n\rightarrow+\infty}(1 + (\frac{x}{n})^\frac{n}{x}
\]

这个不就是上面伯努利一开始发现的常数2.718嘛。所以exp(x)最后可以写成:

\[exp(x) = e ^x
\]

这也就是指数函数最早的由来，e也是从这里来的，所以e也叫欧拉常数。这个式子的意义是说，通过不断结算的方式追求到的复利也是有极限的，他的极限就是e^x倍。x指年利率。

计算机为什么是二进制？

乍一看这个问题很突兀，为什么计算机是二进制，一般这个问题的答案都是因为电荷只有正电荷和负电荷，所以计算机里面一个电子元器件只能表示两种状态，然后就用二进制了。但是你有没有想过，如果我把好几个电子元器件捆绑在一块，比如我捆绑三个元器件，这样这三个元器件就可以表示0到7的数，这样咱们直接搞个8进制不也可以嘛？这里就涉及到信息表示效率了，信息的表示效率指的是能表示的信息量于表示这个信息量所需要的资源的比值。比如举2进制的例子来说，现在要表示0到7这个数据量，那么我们用3个二进制单元就可以表示完了。所以我们站在数学的角度推广这个结论，就是我们要表示m个数，那么在二进制下面要用n个二进制单元去表示，也就是

\[m = 2 ^n
\]

那么在二进制下面要表示那么多数需要多少种状态呢，每个比特位就是两种状态嘛。所以一共需要：

\[s = 2n
\]

那么这个时候我们把这个结论推广成x进制，看看谁的效率是最高的。m个数要是在x进制下面表示就就是：

\[m = x ^ n
\]

那么他需要的资源就是

\[s = xn
\]

那么这里我们讨论的就应该是在表示相同数据量m的时候，那个进制，也就是x的值，会使得s是最小的。这样子就最省资源了，这就是效率最高的做法。那么我们把这两个式子联合起来计算，从第一个式子中得到

\[n = \frac{lnm}{lnx}
\]

代入到第二个式子就会得到：

\[s = lnm * \frac{r}{lnr}
\]

m是常数，所以这个式子什么时候最小取决于r/lnr什么时候最小。这个就比较好做了，对这个式子进行求导会发现这个式子在r取e的时候会取得最小值。所以理论上来说e进制效率是最高的，e的取值是2.718所以理论上来说三进制应该比二进制更高效。但是不好实现，实在没有合适的运算逻辑和简易的实现方式。所以选择了二进制。后来也有人研究三进制，但是等他们优化了三进制的逻辑运算之后，二进制的计算机已经普及了，当你要起跑的时候你的对手已经跑的没影了。。。不过后面三进制有没有弯道超车的机会也未可知，这也是科技的魅力。。

总结

其实写下这篇文章也是机缘巧合，也不知道为什么可以看书看着看着就兴冲冲的研究起来。但是在内心中还是为学到了东西而感到快乐的，希望把这份快乐也传递给你。另外也推荐《数学极客》这本书给你，个人感觉写的蛮不错的。

参考资料

一次看懂自然常数e的由来：https://www.bilibili.com/video/BV1Ds41177ZS?share_source=copy_web
自然对数到底有多自然：https://zhuanlan.zhihu.com/p/144289699

个人推广

下面是笔者的公众号，希望兄弟们可以多多关注，感谢您的支持啦～