李雅普诺夫方法参考

 

6_稳定性_李雅普诺夫_Lyapunov的更多相关文章

  1. ECMA Script 6_字符串_扩展_字符 是4字节还是2字节？_模板字符串

    ES6 字符串扩展 ES6 加强了对 Unicode 的支持,并且扩展了字符串对象 字符 的 Unicode 表示法 允许采用 \uxxxx 形式表示一个字符, 其中 xxxx 表示字符的 Unico ...

  2. 现代控制理论习题解答与Matlab程序示例

    现代控制理论习题解答与Matlab程序示例 现代控制理论 第三版 课后习题参考解答: http://download.csdn.net/detail/zhangrelay/9544934 下面给出部分 ...

  3. 佛祖保佑 永无BUG ; 心外无法 法外无心

    登录linux命令行后出现的图形 复制图形代码到相应的文件中保存,重新登录即可出现. Usage: For Ubuntu: 12.04: Just copy the content from Budd ...

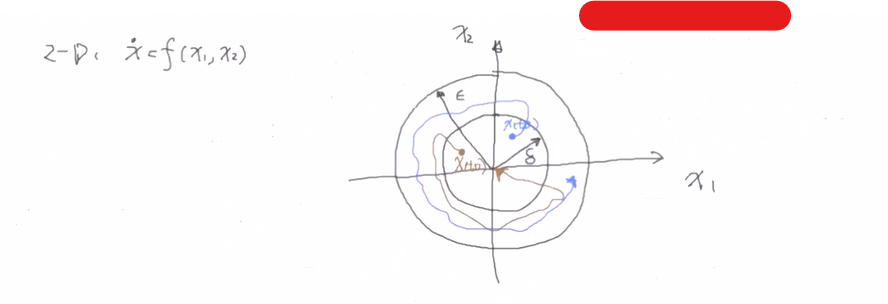
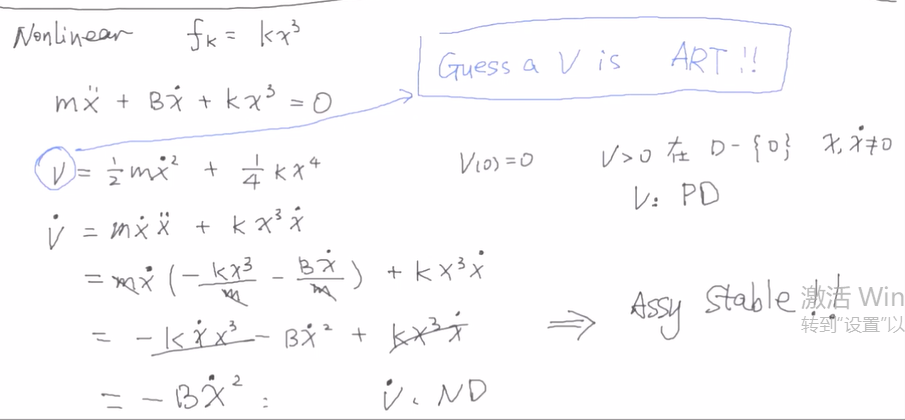
  4. 李雅普诺夫函数 LyapunovFunction 李雅普诺夫意义下的稳定性

    https://zh.wikipedia.org/zh-hans/李亞普諾夫函數 李雅普诺夫函数(Lyapunov function)是用来证明一动力系统或自治微分方程稳定性的函数.其名称来自俄罗斯数 ...

  5. 2_稳定性分析_极点_Stability

    在复平面内 控制理论就是设计控制器D使输入输出之间的传递函数的极点落在复平面的左侧,在现代控制理论中研究状态矩阵的特征值判断稳定性

  6. ECMA Script 6_数组的扩展_扩展运算符

    1. 扩展运算符 内部调用的是数据结构的 Iterator 接口, 因此只要具有 Iterator 接口的对象,都可以使用扩展运算符 ... 如 map,,,, [...arr] 扩展运算符(spre ...

  7. ECMA Script 6_解构赋值_模式匹配

    解构赋值 从数组中提取值,按照对应位置,对变量赋值 只要等号右边的值不是对象或数组,就先将其转为对象. 由于 undefined 和 null 无法转为对象,所以对它们进行解构赋值,都会报错 let ...

  8. Android客户端稳定性测试——Monkey

    修改时间 修改内容 修改人 2016.6.20 创建 刘永志 2016.6.29 完成 刘永志 Monkey简介: Android SDK自带的命令行测试工具,向设备发送伪随机事件流,对应用程序进行进 ...

  9. 易语言关于使用CURL，网页_访问,网页_访问S,网页_访问_对象,鱼刺（winHttpW）发送Get性能测试

    易语言关于使用 CURL,网页_访问,网页_访问S,网页_访问_对象,鱼刺(winHttpW)发送Get性能测试 测试模块情况: |-精易模块5.8  |-鱼刺类Http  |-libCURL +++ ...

随机推荐

  1. StackExchange.Redis 实现SetNx

    今天有同事指出如何在StackExchange.Redis 实现Redis的原生命令. ConnectionMultiplexer redis = ConnectionMultiplexer.Conn ...

  2. 携程applo配置

    1.官网文档 https://github.com/ctripcorp/apollo/wiki/%E5%88%86%E5%B8%83%E5%BC%8F%E9%83%A8%E7%BD%B2%E6%8C% ...

  3. Higncharts 制作

    <html> <head> <meta charset="UTF-8" /> <title>Highcharts 教程 | 菜鸟教程 ...

  4. laravel7 H-ui模板ajax软删除

    1:HTML 书写 {{-- 不能自己删除自己的按钮出现 $item循环的值,$auth检测函数 --}} @if(auth()->id()!=$item->id) <a title ...

  5. Java安全第一篇 ｜ 反射看这一篇就够了

    什么是反射? Java安全可以从反序列化漏洞说起,反序列化漏洞又可以从反射说起.反射是⼤多数语⾔⾥都必不可少的组成部分,对象可以通过反射获取他的类,类可以通过反射拿到所有⽅法(包括私有),拿到的⽅法可 ...

  6. 一些Docker 操作集合

    基本 显示所有容器(包括已停止): docker container ls -a 删除所有容器: docker stop $(docker ps -q) docker rm $(docker ps - ...

  7. asp.net多语言网站的完整解决方案

    应用场景:通过前端切换网站使用英语.中文两种语言. 解决思路:ResourceManager会通过当前线程区域性信息,读取对应的Resource文件,从而达到切换语言的效果,其实质是是在切换当前线程的 ...

  8. mysql索引失效原理（联合索引失效问题）

    单值索引B+树图单值索引在B+树的结构里,一个节点只存一个键值对 联合索引开局一张图,由数据库的a字段和b字段组成一个联合索引. 从本质上来说,联合索引也是一个B+树,和单值索引不同的是,联合索引的键 ...

  9. 文档类型声明<!DOCTYPE html>

    <!DOCTYPE HTML PUBLIC "-//W3C//DTD HTML 4.01 Transitional//EN" "http://www.w3.org/ ...

  10. mysql主从异步复制过程

    mysql是现在普遍使用的数据库,但是如果宕机了必然会造成数据丢失.为了保证mysql数据库的可靠性.就要会一些提高可靠性的技术. 主从复制原理如下. slave(从服务器) master(主服务器) ...