【LeetCode】剑指 Offer 30. 包含min函数的栈

题目描述

定义栈的数据结构，请在该类型中实现一个能够得到栈的最小元素的 min 函数在该栈中，调用 min、push 及 pop 的时间复杂度都是 O(1)。

思路

最初看到O(1)复杂度的时候，就想直接用一个min变量保存当前最小值，后来想到弹栈弹出的有可能是最小值，那么只能用辅助栈。

我的代码如下

class MinStack {
    public Stack<Integer> minVal;//辅助栈
    public Stack<Integer> s;//主栈
    /** initialize your data structure here. */
    public MinStack() {
        minVal=new Stack<Integer>();
        s=new Stack<Integer>();
    }

    public void push(int x) {
        s.push(x);
        if(s.size()==1)//第一个元素入栈的时候，直接进入minVal
        {
            minVal.push(x);
        }
        else{//将当前元素与min值比较，如果小于等于min值，就入minVal栈中
            int p=minVal.peek();
            if(x<=p){//一定要加等号：如果有两个最小值，pop一个，还剩一个
                minVal.push(x);
            }
        }
    }

    public void pop() {
        if(s.size()==0) ;
        int k=s.pop();
        int p=minVal.peek();
        if(k==p){//若主栈弹出的元素是最小值就弹minVal栈
            minVal.pop();
        }
    }

    public int top() {
        if(s.size()==0) return -1;
        return s.peek();
    }

    public int min() {
        if(minVal.size()==0) return -1;
        return minVal.peek();
    }
}

/**
 * Your MinStack object will be instantiated and called as such:
 * MinStack obj = new MinStack();
 * obj.push(x);
 * obj.pop();
 * int param_3 = obj.top();
 * int param_4 = obj.min();
 */

改进思路

改进解法：只需要一个栈

思路

依然设置一个min变量记录当前最小值，但是当元素b(b<min)入栈时，需要做两步：

1.min入栈

2.b入栈

那么在弹栈时，若将要弹出的是当前min，就把min设置为栈顶下面的元素，然后别忘了再pop一下。（可以直接写min=s.pop()，一句话两个操作）

图解（源自LeetCode用户@数据结构和算法)：

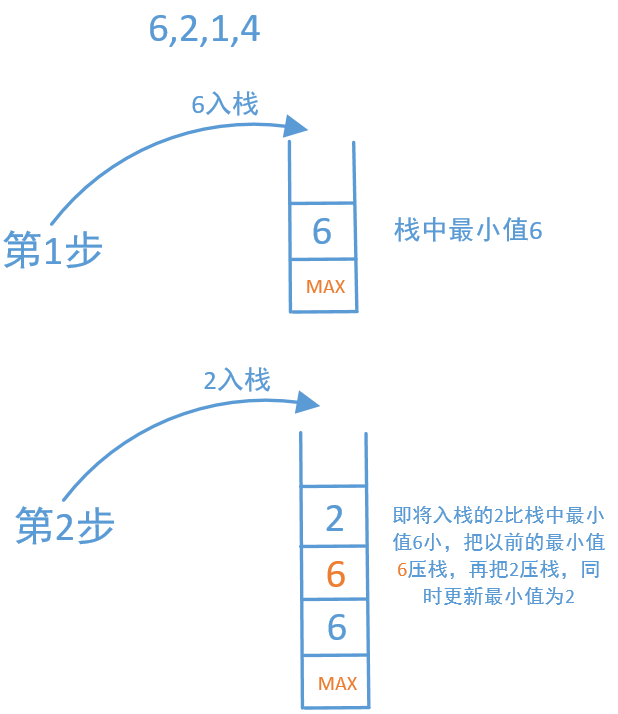
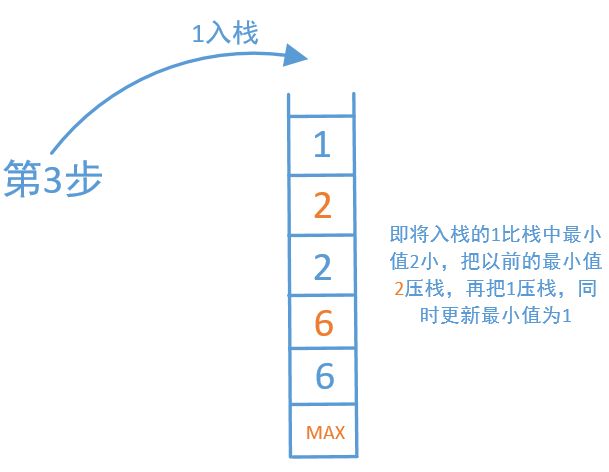
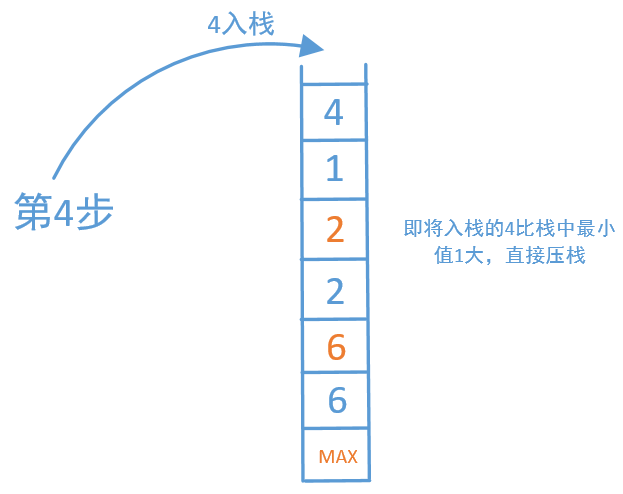
代码

class MinStack {//push方法可能会加入很多min
    int min = Integer.MAX_VALUE;
    Stack<Integer> stack = new Stack<>();

    public void push(int x) {
        //如果加入的值小于最小值，要更新最小值
        if (x <= min) {
            stack.push(min);
            min = x;
        }
        stack.push(x);
    }

    public void pop() {
        //如果把最小值出栈了，就更新最小值
        if (stack.pop() == min)
            min = stack.pop();
    }

    public int top() {
        return stack.peek();
    }

    public int min() {
        return min;
    }
}

更优改进解法：压入当前值和min的差值

思路

由于上面改进思路存在这样的不足，即如果输入的是一个递减序列，那么每次都需要将min入栈，占用空间较大；为了改进这个问题，可以不压入当前值，而是压入当前值与min的差值，pop时，若pop的是负数，说明最小值已经出栈了，重新更新最小值。

弹栈的时候分两种情况：

1.pop出来的是个负数，说明此数应该是当前最小值，直接返回min即可

2.pop出来的是个正数a，说明此数比当前min大a,返回min+a

代码

public class MinStack {
    long min;
    Stack<Long> stack = new Stack<>();

    public void push(int x) {
        if (stack.isEmpty()) {
            stack.push(0L);//最初设最小值为x,所以最小值与x的差值直接是0
            min = x;
        } else {
            //这里入栈的是入栈的值和最小值的差值，有可能为负，也有可能为正。
            stack.push(x - min);
            if (x < min)
                min = x;
        }
    }

    public void pop() {
        if (stack.isEmpty())
            return;
        long pop = stack.pop();
        //因为入栈的是差值，当出栈的为负数的时候，说明栈中最小值已经出栈了，
        //这里要重新更新最小值
        if (pop < 0)
            min -= pop;
    }

    public int top() {
        long top = stack.peek();
        if (top > 0) {
            //栈顶元素如果是正的，说明栈顶元素压栈的时候是比栈中最小值大的，根据
            //top=x - min，可以计算x=top+min
            return (int) (top + min);
        } else {
            //当栈顶元素是负数的时候，说明栈顶元素压栈的时候是比栈中最小值小的，
            //而压栈完之后他会更新最小值min，所以如果在使用上面公式肯定是不行
            //的。如果栈顶元素压栈的时候比最小值小，他会更新最小值，这个最小值
            //就是我们要压栈的值，所以这里直接返回min就行了。
            return (int) (min);
        }
    }

    public int min() {
        return (int) min;
    }
}