CF1098D 题解

题意

传送门

对于一个元素个数大于 \(1\) 的可重集，每次取出两个数 \(x,y\) 合并。若 \(x\le y\le 2x\)，则称其为危险合并。重复上述操作至无法合并。

给你一个初始为空的可重集与 \(n\) 次操作，每次加入或删除一个数，求每次操作后最大的危险合并次数。

\(1\le n \le5\times10^5,1\le x\le10^9\)。

题解

这题太妙了。深深感觉自己的弱小……

首先我们证明一个结论：每次取最小的两个数合并，可以取得最大的危险合并次数。方便起见，称 \(x,y\) 是危险合并为 \(x,y\) 合法。

设最小两值为 \(a,b\)。若不合并 \(a,b\)，那么 \(a,b\) 中先与其他数合并的那个，不妨设为 \(b\)。考虑 \(b,c\) 合并，其中 \(c\geq b\)：

• 若 \(b,c\) 合法。若 \(a+b\le c\)，则显然 \(a+b,c\) 合法。若 \(a+b>c\)，由 \(a\le c,b\le c\)，有 \(a+b\le2c\)，则 \(a+b,c\) 也合法。那么贪心先合并 \(a,b\)。
• 若 \(b,c\) 不合法。因为 \(2b<c\)，所以 \(a+b<c\)。显然先合并 \(a,b\) 不会更劣。

于是不带修直接用小根堆即可。那么带修呢？

再证明一个结论：若最小二值 \(a,b\) 合法，则接下来的所有合并 \(x,y\)，若 \(x,y\in[b,a+b]\)，则 \(x,y\) 合法。

证明很简单，\(y\le2x\iff y-x\le x\)，因为 \(y-x\le a\)，故成立。有了这个结论，我们可以做很多事。

我们可以证明，将初始元素升序排序后，合法合并一定是一段段的。如下（图片来自 \(\texttt{lzqy_}\)）

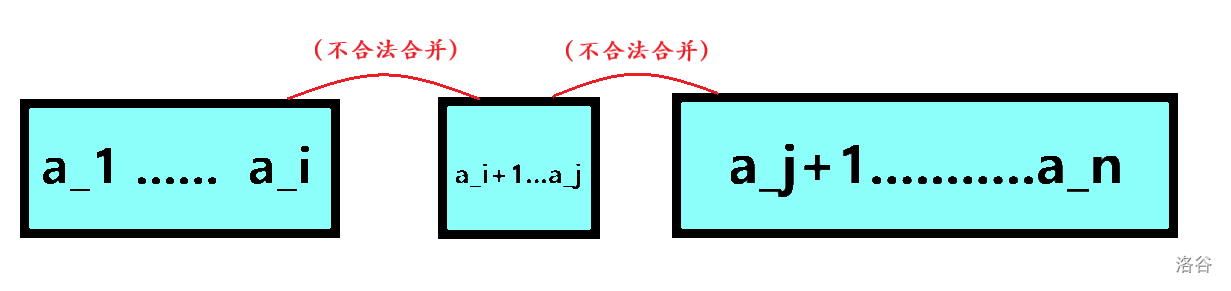
且所有不合法合并一定是形如 \(2\sum\limits_{i=1}^{x-1}a_i<a_{x}\)。于是我们就将原来动态的合并转化为了静态问题。

按值域分块，\([2^0,2^1),[2^1,2^2)\cdots[2^{29},2^{30})\)。则每块内只有第一个元素可能非法。逐块判断即可。复杂度 \(O(n\log x)\)。