w

待处理

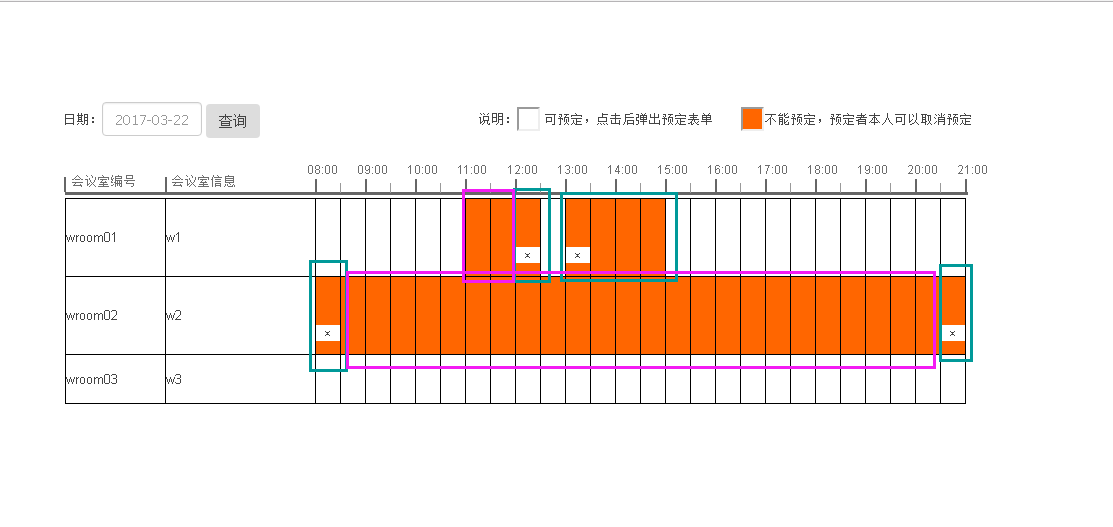
会议室预订 - 对td的处理以区分预订者的更多相关文章

  1. 会议室预订系统 td 宽度 php 浏览器 兼容性

    w获取浏览器标识 <style> .w > td { <?php $wua=$_SERVER['HTTP_USER_AGENT']; if(strpos($wua, 'Chro ...

  2. 会议室预订系统(meeting room booking system)

    一.mrbs mrbs:(meeting room booking system) 二.效果   三.models from django.db import models # Create your ...

  3. jQuery遍历Table tr td td中包含标签

    function shengchen() { var arrTR = $("#tbModule").children(); var Context=""; $( ...

  4. yarn的学习之2-容量调度器和预订系统

    本文翻译自 http://hadoop.apache.org/docs/r2.8.0/hadoop-yarn/hadoop-yarn-site/CapacityScheduler.html 和http ...

  5. [App Store Connect帮助]七、在 App Store 上发行（2.2）设定价格与销售范围：将您的 App 以预订形式发布

    在首次将您的 App 发布至 App Store 前,您可以选择以预订形式提供该 App.在您的 App 发布以供下载之前,顾客可以查看您的产品页并订购您的 App.您的 App 一旦发布,顾客将会收 ...

  6. mrbs - 初识

    一.mrbs mrbs:(meeting room booking system)会议室预订系统 二.效果 三.models from django.db import models # Create ...

  7. order meeting room - 离散度30min

    w <meta charset="UTF-8"> <?php include('conn.php'); include('w_fun.php'); include ...

  8. UML基础与Rose建模实训教程

    目  录 第1章  初识UML. 1 1.1 初识UML用例图... 1 1.2 初识UML类图... 3 第2章  Rational Rose工具... 6 2.1 安装与配置Rational Ro ...

  9. python 学习笔记十四 jQuery案例详解（进阶篇）

    1.选择器和筛选器 案例1 <!DOCTYPE html> <html lang="en"> <head> <meta charset=& ...

随机推荐

  1. 转：python之如何在某文件中调用其他文件内的函数

    假设名为A.py的文件需要调用B.py文件内的C(x,y)函数 情形1:在同一目录下, (1) import B if __name__ == "__main__": B.C(x, ...

  2. 735. Replace With Greatest From Right【medium】

    Given an array of integers, replace every element with the next greatest element (greatest element o ...

  3. iOS图片上传及压缩

    提到从摄像头/相册获取图片是面向终端用户的,由用户去浏览并选择图片为程序使用.在这里,我们需要过UIImagePickerController类来和用户交互. 使用UIImagePickerContr ...

  4. Itunes connect上传应用视频 app preview时遇到“无法载入文件”的问题

    总结一下,上传视频的一个经验吧,在使用safari进行上传的时候,有时出现了问题,上传失败,但是提示语只有一句“无法载入文件,请再次尝试”.这样的提示并不能提供更多的信息,为什么视频无法上传.有这样的 ...

  5. C++忽略字符大小写比较

    在项目中用到对两个字符串进行忽略大小写的比较,有两个方法实现 1.使用C++提供的忽略大小写比较函数实现 代码实现: /* 功能 :忽略大小写进行字符串比较 */ #ifdef __LINUX__ # ...

  6. uGUI ScrollView

    Scroll View + Grid Layout Group 滑动列表,与NGUI类似 ScrollView上所需组件:Scroll Rect + Mask + Image.Scroll Rect指 ...

  7. python笔记4 - 函数

    函数是组织好的,可重复使用的,用来实现单一,或相关联功能的代码段. 函数能提高应用的模块性,和代码的重复利用率.你已经知道Python提供了许多内建函数,比如print().但你也可以自己创建函数,这 ...

  8. 设置EntityFramework中decimal类型数据精度

    EF中默认的decimal数据精度为两位数,当我们数据库设置的精度大于2时,EF将只会保留到2为精度. e.g. 2.1999将会被保存为2.20 网上找到常见的方法为重写DbContext的OnMo ...

  9. Img src用base64数据

    <img src='data:image/jpeg;base64,/9j/4AAQSkZJRgABAQAAAQABAAD/2wBDAAMCAgICAgMCAgIDAwMDBAYEBAQEBAgG ...

  10. php form 图片上传至服务器上

    本文章也是写给自己看的,因为写的很简洁,连判断都没有,只是直接实现了能上传的功能. 前台: <form action="upload.php" method="PO ...