【bzoj3476-懒惰的奶牛】线段树

题解：

感觉这题和别人的做法不一样。。。呵呵呵。。。调了一百年。。

设家坐标为（a,b），对于每个点（x,y），可以转化为|a-x|+|b-y|<=k

对于每个点，它的影响范围是一个菱形（也就是一个正方形啦。。），也就是一个图上有若干个正方形。

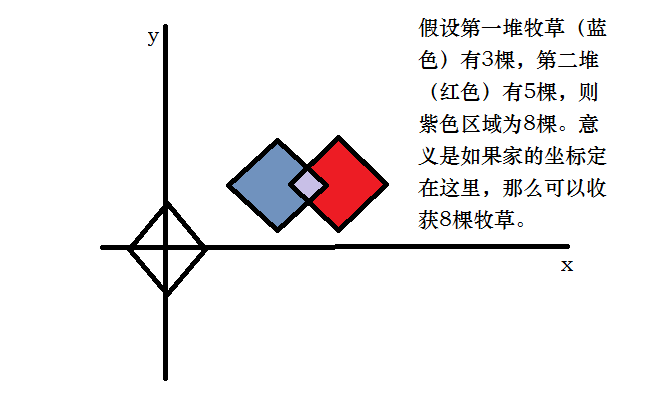
然后我就把这个坐标轴选择了45度。

好难画不画了，正交分解一下就可以了。

然后题目就转化成正方形各种交里的最大值。

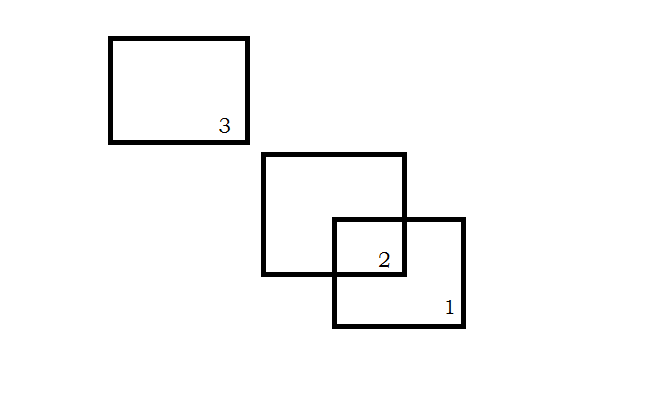
正方形有x和y两个元素，但是很明显我们只能维护一个。。

所以我以x轴建立线段树，对于每个正方形按照y从小到大排序。

维护一个指针j，表示当前前j个正方形已经和现在在处理的第i个正方形没有交集。每次都要先把j更新（看看它是否能后移）。

然后我们在当前正方形的两端a[i].x~a[i].y这一段+a[i].d

每个点维护当前的和d以及该区间的最大值mx。每次做完之后，用t[1].mx更新答案。

 #include<cstdio>
 #include<cstdlib>
 #include<cstring>
 #include<iostream>
 #include<ctime>
 #include<queue>
 #include<algorithm>
 using namespace std;

 const int N=,INF=(int)1e9;
 int n,K,L,tl,ans;
 struct trnode{
     int l,r,lc,rc,d,mx,lazy;
 }t[*N];
 struct node{
     int x,y,d;
 }a[N];

 bool cmp(node x,node y){return x.y<y.y;}
 int maxx(int x,int y){return x>y ? x:y;}
 int minn(int x,int y){return x<y ? x:y;}

 int read()
 {
     int x=,f=; char ch=getchar();
     while(ch<''||ch>''){if(ch=='-')f=-; ch=getchar();}
     while(ch>=''&&ch<=''){x=x*+ch-''; ch=getchar();}
     return x*f;
 }

 int bt(int l,int r)
 {
     int x=++tl;
     t[x].l=l;t[x].r=r;
     t[x].lc=t[x].rc=;
     t[x].mx=;t[x].d=;
     t[x].lazy=;
     if(l<r)
     {
         int mid=(l+r)/;
         t[x].lc=bt(l,mid);
         t[x].rc=bt(mid+,r);
     }
     return x;
 }

 void pd(int x)
 {
     if(t[x].lazy==) return ;
     int d=t[x].lazy,lc=t[x].lc,rc=t[x].rc;
     t[x].lazy=;
     t[x].d+=d;
     t[x].mx+=d;
     if(lc) t[lc].lazy+=d;
     if(rc) t[rc].lazy+=d;
 }

 void change(int x,int l,int r,int d)
 {
     pd(x);
     if(t[x].l==l && t[x].r==r)
     {
         t[x].lazy+=d;
         pd(x);
         return ;
     }
     int lc=t[x].lc,rc=t[x].rc,mid=(t[x].l+t[x].r)/;
     if(r<=mid) change(lc,l,r,d);
     else if(l>mid) change(rc,l,r,d);
     else
     {
         change(lc,l,mid,d);
         change(rc,mid+,r,d);
     }
     pd(x);pd(lc);pd(rc);
     t[x].mx=maxx(t[lc].mx,t[rc].mx);
 }

 int main()
 {
     // freopen("a.in","r",stdin);
     // freopen("me.out","w",stdout);
     freopen("lazy.in","r",stdin);
     freopen("lazy.out","w",stdout);
     n=read();K=read();
     // scanf("%d%d",&n,&K);
     int x,y,tx,ty,nx=INF,ny=INF,mx=;tl=;L=*K;
     for(int i=;i<=n;i++)
     {
         a[i].d=read();x=read();y=read();
         // scanf("%d%d%d",&a[i].d,&x,&y);
         tx=x,ty=y+K;
         a[i].x=tx-ty;
         a[i].y=tx+ty;

         nx=minn(nx,a[i].x);
         ny=minn(ny,a[i].y);
     }
     for(int i=;i<=n;i++)
     {
         a[i].x-=nx-;
         a[i].y-=ny-;
         mx=maxx(mx,a[i].x);
     }
     mx+=;ans=;
     sort(a+,a++n,cmp);
     bt(,mx);
     int j=;
     change(,a[].x,minn(mx,a[].x+L),a[].d);
     ans=maxx(ans,t[].mx);
     for(int i=;i<=n;i++)
     {
         while(j<i && a[i].y-L>a[j].y)
         {
             change(,a[j].x,minn(mx,a[j].x+L),-a[j].d);
             ans=maxx(ans,t[].mx);
             j++;
         }
         change(,a[i].x,minn(mx,a[i].x+L),a[i].d);
         ans=maxx(ans,t[].mx);
     }
     printf("%d\n",ans);
     return ;
 }