C++写矩阵的转置

　　(2019年2月19日注：这篇文章原先发在自己github那边的博客，时间是2017年2月5日)

　　对于任意非n阶矩阵的转置，用c++应该怎么写代码，思考了一下，发现并没有那么简单，上网找到了一个比较好的算法，叫做矩阵原地转置矩阵算法。基于别人的代码，改写成可以使用指针动态分配内存的方法。

　　先放传送门：C++实现矩阵原地转置算法的实现

　　原理并不难，那篇文章非常的详细，我不再赘述，下面把改写好的代码发出来。

 /*************************************************************************
 > File Name: matrix_transpose.cpp
 > Author: SongLee
 > Modified: JCChan
 ************************************************************************/
 #include<iostream>
 using namespace std;
 /* 后继 */
 int getNext(int i, int m, int n)
 {
     return (i%n)*m + i / n;
 }
 /* 前驱 */
 int getPre(int i, int m, int n)
 {
     return (i%m)*n + i / m;
 }
 /* 处理以下标i为起点的环 */
 void movedata(int *mtx, int i, int m, int n)
 {
     int temp = mtx[i]; // 暂存
     int cur = i;    // 当前下标
     int pre = getPre(cur, m, n);
     // 从最后一个数开始，获得它的前驱，直到前驱的值和最后一位值相等，相当于交换的逆过程
     while (pre != i)
     {
         mtx[cur] = mtx[pre];
         cur = pre;
         pre = getPre(cur, m, n);
     }
     mtx[cur] = temp;
 }
 /* 转置，即循环处理所有环 */
 void transpose(int *mtx, int m, int n)
 {
     for (int i = ; i<m*n; ++i)
     {
         int next = getNext(i, m, n);
         while (next > i) // 若存在后继小于i说明重复
             next = getNext(next, m, n);
         if (next == i)  // 处理当前环
             movedata(mtx, i, m, n);
     }
 }
 void input(int *mtx, int row, int column) {
     for (int i = ; i < row; i++) {
         for (int j = ; j < column; j++) {
             cout << "请输入矩阵的第" << i +  << "行第" << j +  << "个元素：";
             //    根据矩阵的坐标推算它在一维数组中的位置。
             cin >> *(mtx + column*i + j);
         }
     }
 }
 /* 输出矩阵 */
 void print(int *mtx, int m, int n)
 {
     for (int i = ; i<m*n; ++i)
     {
         if ((i + ) % n == )
             cout << mtx[i] << "\n";
         else
             cout << mtx[i] << " ";
     }
 }
 /* 测试 */
 int main()
 {
     int row, column;
     cout << "请输入矩阵的行数：";
     cin >> row;
     cout << "请输入矩阵的列数：";
     cin >> column;
     int *matrix = new int[row*column];
     input(matrix, row, column);
     cout << "Before matrix transposition:" << endl;
     print(matrix, row, column);
     transpose(matrix, row, column);
     cout << "After matrix transposition:" << endl;
     print(matrix, column, row);
     delete[] matrix;
     system("pause");
     return ;
 }

　　结果如下

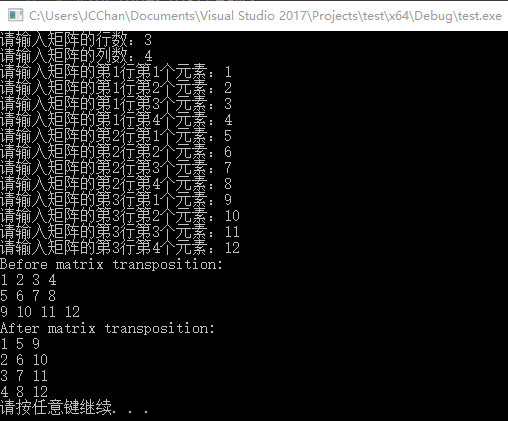
　　对于n阶方阵来说，情况则简单的多，同样放上代码。

 #include<iostream>
 using namespace std;
 void move(int *matrix, int n)
 {
     int i, j, k;
     for (i = ; i<n; i++)
         for (j = ; j<i; j++)
         {
             k = *(matrix + i*n + j);
             *(matrix + i*n + j) = *(matrix + j*n + i);
             *(matrix + j*n + i) = k;
         }
 }
 int main()
 {
     int n, i, j;
     int *p;
     cout << "请输入矩阵的维数：";
     cin >> n;
     p = new int[n*n];
     cout << "输入矩阵的元素" << endl;
     for (i = ; i<n; i++)
         for (j = ; j<n; j++)
         {
             cout << "第" << i +  << "行第" << j +
                 << "个元素为：";
             cin >> p[i*n + j];
         }
     cout << "输入的矩阵的为：" << endl;
     for (i = ; i<n; i++)
     {
         for (j = ; j<n; j++)
             cout << p[i*n + j] << " ";
         cout << endl;
     }
     move(p, n);
     cout << "转置后的矩阵的为：" << endl;
     for (i = ; i<n; i++)
     {
         for (j = ; j<n; j++)
             cout << p[i*n + j] << " ";
         cout << endl;
     }
     delete[] p;
     system("pause");
     return ;
 }