c++ 贪心讲解大礼包
贪心是什么?
它其实类似一种思想
就是总问题可以分成许多的子问题
子问题的最优解可以直接推出整个问题
它和动态规划有一定的不同之处 动态规划不能由子问题的最优解推出整个问题的最优解 所以你看都要有一个数组来记录一下嘛
贪心怎么用?
就是说我们把整个问题分成许多的子问题
然后对子问题求得局部最优解
几个简单的例子?
【例1】
n个人打水,每个人用的时间是t1, t2, t3… 现在有m水龙头,问所有人等待时间总和最小.
解:很显然 这一道题我们就要让时间t更短的人先打水 这样子后面的人就可以少等一点时间 这就是一个贪心的思想
【例2】
给定数轴上的很多区间,求尽量多的区间,使得他们两两不相交.
解:这一题倒是比较值得品味一下的 假如这些区间是这个样子的
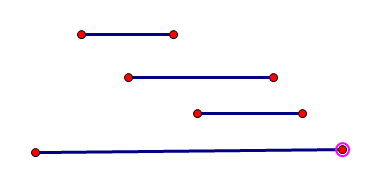
这里有4条线段 我们按照右端点来排序
右端点最靠前的是1号线段 然后我们在剩下的线段里找满足要求(没有交集)的线段里右端点靠前的线段 这样子剩下的长度多 后面选的线段数也就会更多
(后续内容会持续更新)
c++ 贪心讲解大礼包的更多相关文章
- 洛谷日报 & 原来博客(转载)
震惊,新的功能:可以按Ctrl + F 进行关键字查询. \(update\) on 10.26:把这两个月的日报也加入进去了,并且修复了几个错误. 本文会把小编用过的博客和比较好的博客放在这里. 可 ...
- Luogu Daily & Original Blog (reproduced)
震惊,新的功能:可以按Ctrl + F 进行关键字查询. \(update\) on 10.26:把这两个月的日报也加入进去了,并且修复了几个错误. 本文会把小编用过的博客和比较好的博客放在这里. 可 ...
- - > 贪心基础入门讲解五——任务执行顺序
分析: 本题可以抽象成,从一个整数开始,每次减去a,再加上b (a,b都是正数),要求每次操作都不产生负数. 针对本题a[i] = R[i], b[i] = R[i] – O[i],注意O[i] &l ...
- - > 贪心基础入门讲解二——活动安排问题
有若干个活动,第i个开始时间和结束时间是[Si,fi),只有一个教室,活动之间不能交叠,求最多安排多少个活动? 分析: 我们就是想提高教室地利用率,尽可能多地安排活动.考虑容易想到的几种贪心策略: ( ...
- - > 贪心基础入门讲解三——活动安排问题二
有若干个活动,第i个开始时间和结束时间是[Si,fi),活动之间不能交叠,要把活动都安排完,至少需要几个教室? 分析:能否按照之一问题的解法,每个教室安排尽可能多的活动,即按结束时间排序,再贪心选 ...
- - > 贪心基础入门讲解四——独木舟问题
n个人,已知每个人体重,独木舟承重固定,每只独木舟最多坐两个人,可以坐一个人或者两个人.显然要求总重量不超过独木舟承重,假设每个人体重也不超过独木舟承重,问最少需要几只独木舟? 分析: 一个显然的策略 ...
- - > 贪心基础入门讲解一——完美字符串
约翰认为字符串的完美度等于它里面所有字母的完美度之和.每个字母的完美度可以由你来分配,不同字母的完美度不同,分别对应一个1-26之间的整数. 约翰不在乎字母大小写.(也就是说字母F和f)的完美度相同. ...
- 忙碌的Nova君 (活动安排问题、贪心算法)
题目描述 理论上,Nova君是个大闲人,但每天还是有一大堆事要干,大作业啦,创新杯啦,游戏啦,出题坑人啦,balabala......然而精力有限,Nova君同一时间只能做一件事,并不能一心二用.假设 ...
- POJ 1065 Wooden Sticks / hdu 1257 最少拦截系统 DP 贪心
参考链接:http://blog.csdn.net/xiaohuan1991/article/details/6956629 (HDU 1257 解题思路一样就不继续讲解) POJ 1065题意:给你 ...
随机推荐
- netstat 显示当前网络连接的统计信息
C:\Users\Administrator\Desktop\hsqldb-2.3.2\data>netstat -h Displays protocol statistics and curr ...
- CodeForces 1243"Character Swap (Hard Version)"(multimap)
传送门 •前置知识-multimap的用法 $multimap$ 与 $map$ 的区别在于一个 $key$ 可以对应几个值: 对于 $map$ 而言,一个 $key$ 只能对应一个值,并且按照 $k ...
- BZOJ 4034"树上操作"(DFS序+线段树)
传送门 •题意 有一棵点数为 N 的树,以点 1 为根,且树点有边权. 然后有 M 个操作,分为三种: 操作 1 :把某个节点 x 的点权增加 a . 操作 2 :把某个节点 x 为根的子树中所有点的 ...
- Vue导航栏在特定的页面不显示~
最近写vue项目遇到一些问题,我把导航栏组件放在了app.vue中,让他在每个页面都能显示了,但遇到了一个问题,在登录以及注册页面导航栏是不合理不允许存在的 解决方法: 公共模块的内容可以放在App. ...
- Python--day41--线程锁
1,死锁 死锁代码示例: import time from threading import Lock, Thread noodle_lock = Lock() fork_lock = Lock() ...
- H3C RIPv2的改进
- 提前终止forEach技巧,使用try catch
学习react优化性能的时候,在render之前,生命周期shouldComponentUpdate里判断前后两次数据是否一致,使用了forEach嵌套if语句,如果满足条件想直接break跳出for ...
- Java基础系列8——IO流超详细总结
该系列博文会告诉你如何从入门到进阶,一步步地学习Java基础知识,并上手进行实战,接着了解每个Java知识点背后的实现原理,更完整地了解整个Java技术体系,形成自己的知识框架. 在初学Java时,I ...
- 【Jenkins】构建一个maven项目
一 .Ubuntu18.04安装Maven 官方安装文档:http://maven.apache.org/install.html ①去官网下载maven: ②解压到/opt/maven目录(我安装在 ...
- 【Kubernetes】架构全图
K8s是什么 Kubernetes是Google开源的容器集群管理系统.它构建在Docker技术之上,为容器化的应用提供资源调度.部署运行.服务发现.扩容缩容等一整套功能. K8s能做什么 ①容器的自 ...
