uoj37 主旋律

题意：一个班级n个人，如果a爱b，那么a->b一条有向边。问有多少种删边集合使得图仍然强联通？ n<=15.

 

标程：

 #include<cstdio>
 #include<algorithm>
 #include<cstring>
 #include<bitset>
 using namespace std;
 typedef long long ll;
 const int mod=1e9+;
 const int N=;
 int read()
 {
    int x=,f=;char ch=getchar();
    while (ch<''||ch>'') {if (ch=='-') f=-;ch=getchar();}
    while (ch>=''&&ch<='') x=(x<<)+(x<<)+ch-'',ch=getchar();
    return x*f;
 }
 int n,m,Max,pop[N],pow[N],sum_e[N],to_e[N],f[N],a,b,e[N],ie[N],u[N];
 int lowbit(int x){return x&(-x);}
 int main()
 {
     n=read();m=read();
     for (int i=;i<=m;i++)
     {
        a=read(),b=read();
         e[<<a-]|=<<b-,ie[<<b-]|=<<a-;
     }
    Max=<<n;pow[]=;
    for (int i=;i<Max;i++) pop[i]=pop[i>>]+(i&),pow[i]=(ll)pow[i-]*%mod;
    for (int i=;i<Max;i++)
    {
        int v=lowbit(i);int p=i^v;
       sum_e[i]=sum_e[i^v]+pop[e[v]&i]+pop[ie[v]&i];
         f[i]=pow[sum_e[i]];to_e[i]=;
       for (int j=p;j;j=(j-)&p)
            u[i]=((ll)u[i]-(ll)f[i^j]*u[j]%mod+mod)%mod;
        for (int j=i;j;j=(j-)&i)
       {
           int v=lowbit(i^j);to_e[j]=to_e[j|v]-pop[e[v]&(i^j)]+pop[ie[v]&j];
            f[i]=((ll)f[i]-(ll)pow[sum_e[i^j]+to_e[j]]*u[j]%mod+mod)%mod;
        }
        u[i]=((ll)u[i]+f[i])%mod;
     }
    printf("%d\n",f[Max-]);
    return ;
 }

技巧：用lowbit(i)取出i中的任意一个元素（注意是移位<<后的）。

题解：状压枚举子集+容斥dp

乍一看只知道状压。。。强联通是什么鬼嘛。。。

考虑一个不强联通的图，至少有一个点的入度为0。

这样就可以容斥啦：全集-不强连通的图数=强联通的图数。

枚举缩点后入度为0的块有多少个，设包含入度为0的块的集合为T。f[S]表示S集合中的点构成强联通图的方案数，g[S][k]表示将S集合分成k个独立块的方案数,u[S][k]表示带容斥系数的g之和。e(S)表示S点集中的边数。e(S,T)表示从S中的点连出向T的边数。

u[S]也可以通过容斥求得。为了不算重，取一个S集中的点v作为连通块部分的必选点。（减号就相当于是连通块个数+1，(-1)^k变号）

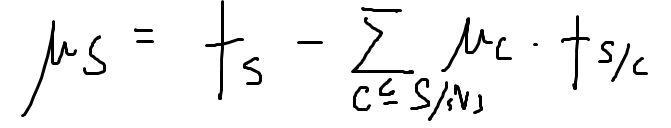
求u和f的时间复杂度都是O(n^3)。求e(S)和e(S,T)都可以通过在子集上累加的方法计算。