清北学堂—2020.1提高储备营—Day 2 afternoon（线段树、树状数组）

qbxt Day 2 afternoon

——2020.1.18 济南主讲：李佳实

目录一览

1.线段树
2.二叉搜索树（略过）
3.树状数组

总知识点：基础数据结构（本人初学感觉好难）

一、线段树

1.描述：线段树是一种分治的思想，用树形结构把一个大区间划分成小区间，它同时又是一棵二叉树。
2.概念名词定义：
区间（又称线段）：线段树上的每一个节点对应于一个区间[a,b]。（a,b为整数）
特殊说明：对于叶子节点，其对应的区间长度为1。

For Example：
（1）区间[1,10]对应的线段树

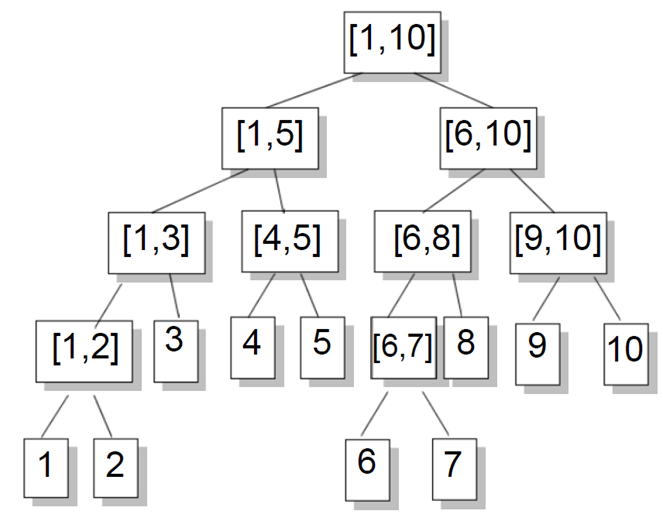
（2）区间[1,9]对应的线段树

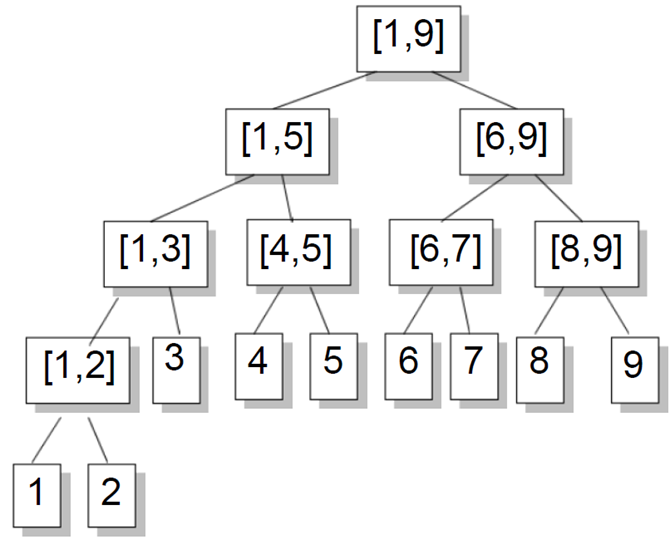
3.性质：对于每一个非叶结点所表示的结点[a,b]，其左儿子表示的区间为[a,(a+b)/2]，右儿子表示的区间为[(a+b)/2+1,b](除法去尾取整）
4.基本操作：
（1）线段树的存储：类似于堆
对于一棵线段树，它的根节点下标为1。
其下标为i的节点，它的左儿子下标为2i，右儿子下标为2i+1。
（2）线段树核心操作：区间分解
定义：若线段树根节点对应区间为[a,b]，给定区间c,d,找出一些节点，使这些节点对应的区间互相不重叠，且加起来正好是[c,d]，这样的操作过程即区间分解。

代码核心思想：二分

操作步骤：（递归分解）
1.从根节点出发，开始区间分解
2.遇到节点[x,y]时，如果要分解的区间就是[x,y]，即为找到一个终止节点，Break。
3.否则，（二分思想）定义mid，取mid=(x+y)/2。
4.看我们要分解的区间与[x,mid]和[mid+1,y]和哪个有交集，就进入区间进行进一步的递归分解。（有可能与左右两个区间都有交集，需要同时分解）
注:区间分解的时间复杂度和分解完以后的区间个数均为O(logn)。

For Example：区间[1,9]的线段树上，分解区间[2,8].

代码实现：

inline void spilt(int k,int l,int r,int z,int y){
        //k为当前节点的编号
    //l,r为线段树的总区间。z,y为要分解的目标区间[z,y]
    if(l==z&&r==y) return;  //找到了一个分解的区间
    int mid=(l+r)/2;
    if(y<=mid) spilt(k*2,l,mid,z,y);    //在左儿子的区间里，分解左儿子的区间
    else if(z>mid) spilt(k*2+1,mid+1,r,z,y);    //在右儿子的区间里，分解右儿子的区间
    else{   //两个区间都有交集
        spilt(k*2,l,mid,z,mid); //目标区间在左儿子里的部分
        spilt(k*2+1,mid+1,r,mid+1,y);   //目标区间在右儿子里的部分
    }
}
//例:(上图)spilt(1,1,9,2,8)

二、二叉搜索树：本内容主要为了以后学习平衡树Tree，暂且略过。。。。。。（勿喷）

三、树状数组：（心碎的回忆）

1.定义：
For Example：
以56为例：56->111000
K=3
56-2^3+1=(110001)(二进制）=49
C[56]=a[49]+..+a[56]
a[1...56]=C[56]+C[48]+C[32]

2.结构

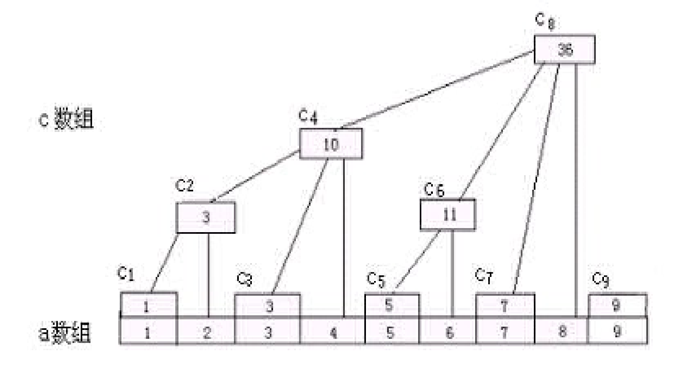
注:A是原数组、C是树状数组。

3.执行操作：单点修改、区间查询
4.（玄学操作）lowbit

2^k=lowbit(x)=x and (x xor(x-1))

For Example:
假设:
x = 0...1...0...10......0（第二个1后k个0）
x = 0...1...0...01......1（第三个0后k个1）
则
x xor(x-1)=0...0...0...11......1（第一个1后k+1个1）
5.查询操作
代码：

int query(int x)    //求a[1...x]的和
{
    int res=0;
    for(int i=x;i>0;i-=lowbit(i)) res+=C[i];
    return res;
}

6.修改操作
代码:
```c++
void add(int x,int delta) //将a[x]添加delta
{
for(int i=x;i<=n;i+=lowbit(i)) C[i]+=delta;
}

---------------------------------------------THE END---------------------------------------------------