POJ 2078 Matrix

Matrix

Time Limit: 2000MS		Memory Limit: 30000K
Total Submissions: 3239		Accepted: 1680

Description

Given an n*n matrix A, whose entries Ai,j are integer numbers ( 0 <= i < n, 0 <= j < n ). An operation SHIFT at row i ( 0 <= i < n ) will move the integers in the row one position right, and the rightmost integer will wrap around to the leftmost column. 

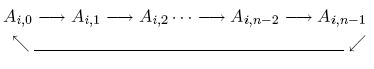
You can do the SHIFT operation at arbitrary row, and as many times as you like. Your task is to minimize 
max_{0<=j< n}{Cj|Cj=Σ_{0<=i< n}A_i,j}

Input

The input consists of several test cases. The first line of each test case contains an integer n. Each of the following n lines contains n integers, indicating the matrix A. The input is terminated by a single line with an integer −1. You may assume that 1 <= n <= 7 and |A_i,j| < 10⁴.

Output

For each test case, print a line containing the minimum value of the maximum of column sums.

Sample Input

2
4 6
3 7
3
1 2 3
4 5 6
7 8 9
-1

Sample Output

11
15
题目大意：一个矩阵每一行的元素都可以循环右移，每次移动后求每个矩阵每一列的和的最大值，然后求所有这些最大值中的最小值。
解题方法：直接暴搜，没啥技巧可言。

#include <stdio.h>
#include <iostream>
#include <string.h>
using namespace std;

int ans = 0x7fffffff;

void Shift(int row, int n, int matrix[][])
{
    int temp = matrix[row][n - ];
    for (int i = n - ; i > ; i--)
    {
        matrix[row][i] = matrix[row][i - ];
    }
    matrix[row][] = temp;
}

void DFS(int index, int n, int matrix[][])
{
    if (index == n)
    {
        return;
    }
    int maxsum = -;
    for (int i = ; i < n; i++)
    {
        int sum = ;
        for (int j = ; j < n; j++)
        {
            sum += matrix[j][i];
        }
        if (sum > maxsum)
        {
            maxsum = sum;
        }
    }
    if (maxsum < ans)
    {
        ans = maxsum;
    }
    for (int i = ; i < n; i++)
    {
        Shift(index, n, matrix);
        DFS(index + , n, matrix);
    }
}

int main()
{
    int n;
    int matrix[][];
    while(scanf("%d", &n) != EOF && n != -)
    {
        ans = 0x7fffffff;
        for (int i = ; i < n; i++)
        {
            for (int j = ; j < n; j++)
            {
                scanf("%d", &matrix[i][j]);
            }
        }
        DFS(, n, matrix);
        printf("%d\n", ans);
    }
    return ;
}