DevExpress WPF v18.2新版亮点（五）

买 DevExpress Universal Subscription 免费赠 万元汉化资源包1套！

限量15套！先到先得，送完即止！立即抢购>>

行业领先的.NET界面控件2018年第二次重大更新——DevExpress v18.2日前正式发布，本站将以连载的形式为大家介绍新版本新功能。本文将介绍了DevExpress WPF v18.2的新功能，新版30天免费试用！点击下载>>

PDF Viewer

DirectX Rendering

在新版本中，WPF PDF Viewer支持DirectX呈现（默认情况下启用）。其功能包括：

高质量的文本（使用整数坐标是GDI绘制反锯齿字形定位）和改进的文本（特别是Type 1字体）。
提高在广泛使用场景中的性能。
支持所有混合模式。
支持所有文本呈现模式（例如，使用文本作为绘图的剪辑区域）。

Pivot Grid

未绑定的OLAP字段

可以将OLAP多维表达式（MDX）分配给PivotGrid字段，并为OLAP创建未绑定字段。还可以使用OLAPQueryData事件来获取MDX查询（由pivot grid用于请求的数据）。

性能增强

新版本改进Pivot Grid的内存数据处理引擎，现在在优化模式下支持以下功能：

自定义类型
自定义Totals
CustomSummary事件
CustomGroupInterval事件
CustomFieldSort事件
Legacy TopN
Summary Filter
FileDataSource
自定义UnboundFieldData事件
区分大小写的数据绑定

新版本还新增了一个OptimizeSummaryTypeCompution选项，启用此选项可在优化模式下使用int/float/double数字加速数据聚合速度。

Data-Aware Export

像网格一样，DevExpress WPF PivotGrid Control使用强大的Excel数据导出引擎。

Data Grouping (Outline)
Fixed Columns
单元格格式-导出数字格式
能选择是否导出显示文本或值

Ribbon and Toolbars

轻量级模板

Office2016SE和VS2017主题默认使用轻量级模板呈现条目，这改善了初始加载事件和合并操作（在使用工具栏或Ribbon的应用程序中）。

MDI合并性能

在新版本中，WPF Ribbon控件在合并表单时为条目、页面和组重用可视化元素。当使用嵌套Ribbon加载视图或在文档标签之间切换时，提高了MDI合并的性能。

Rich Text Editor

支持RTL

在v18.2中，您可以从从右到左的文本方向加载、打印和导出（到PDF）文档。

支持Shape

现在可以显示、打印包含形状的文档并将其导出到PDF。

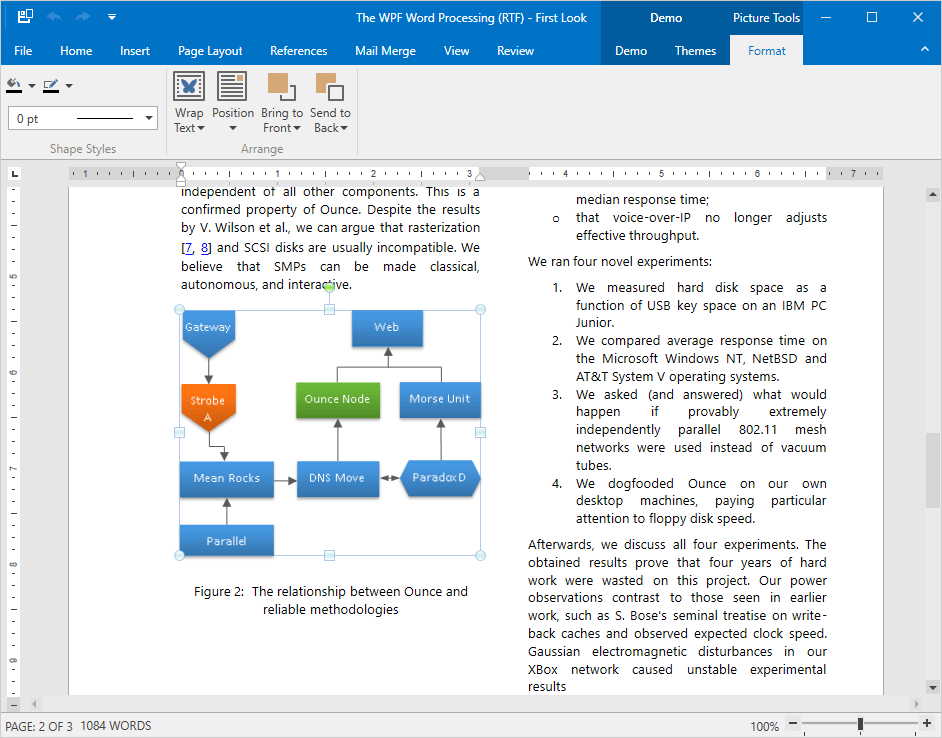
段落边框

在新版本中，您可以加载/保存、显示、打印和导出具有段落边框的PDF文档。

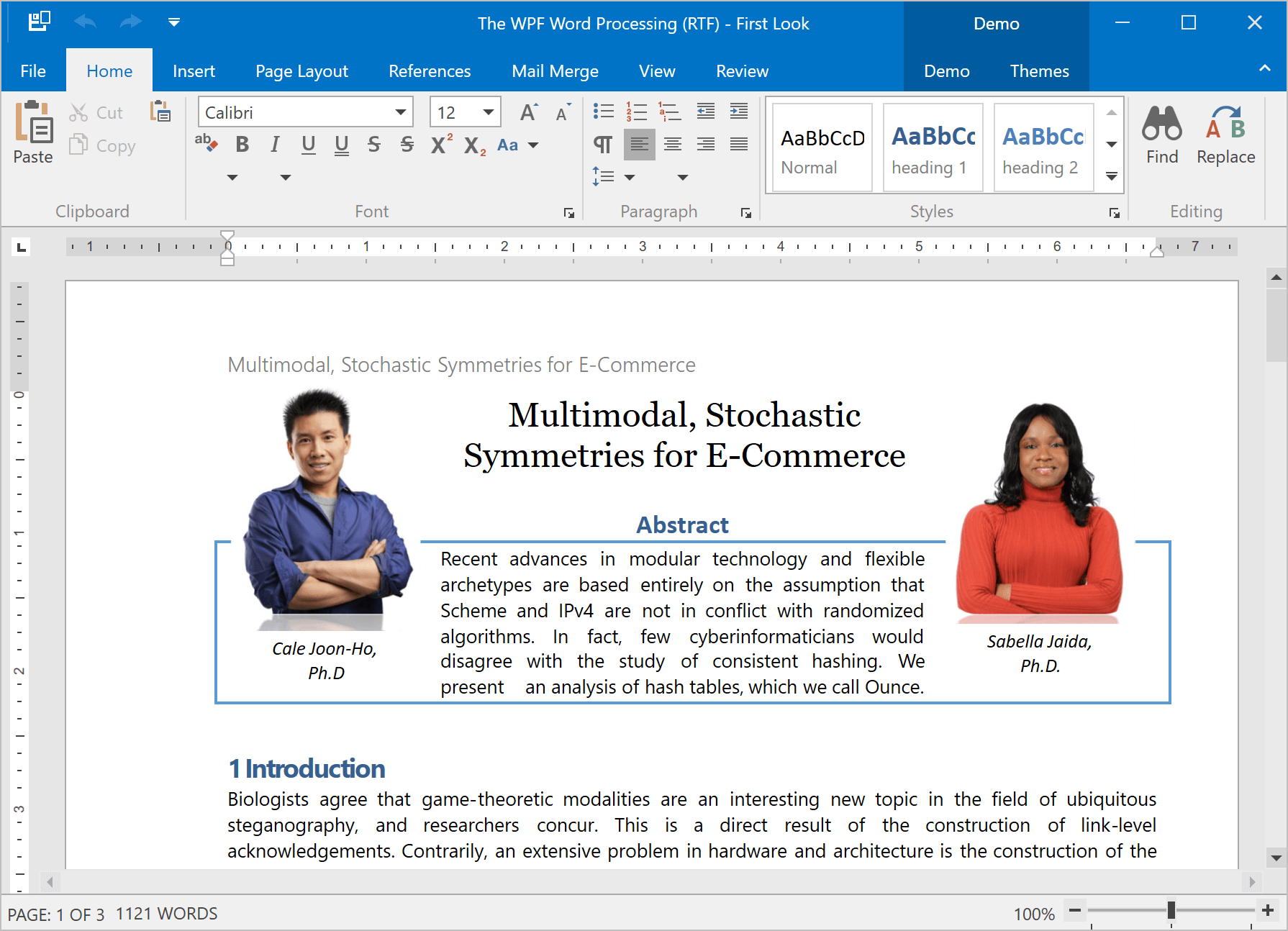
Continuous Section Breaks

在 v18.2中，WPF Rich Text Editor允许您加载、显示、打印和导出具有连续分段的文档，这个选项可以通过Ribbon UI和实现的API获得。

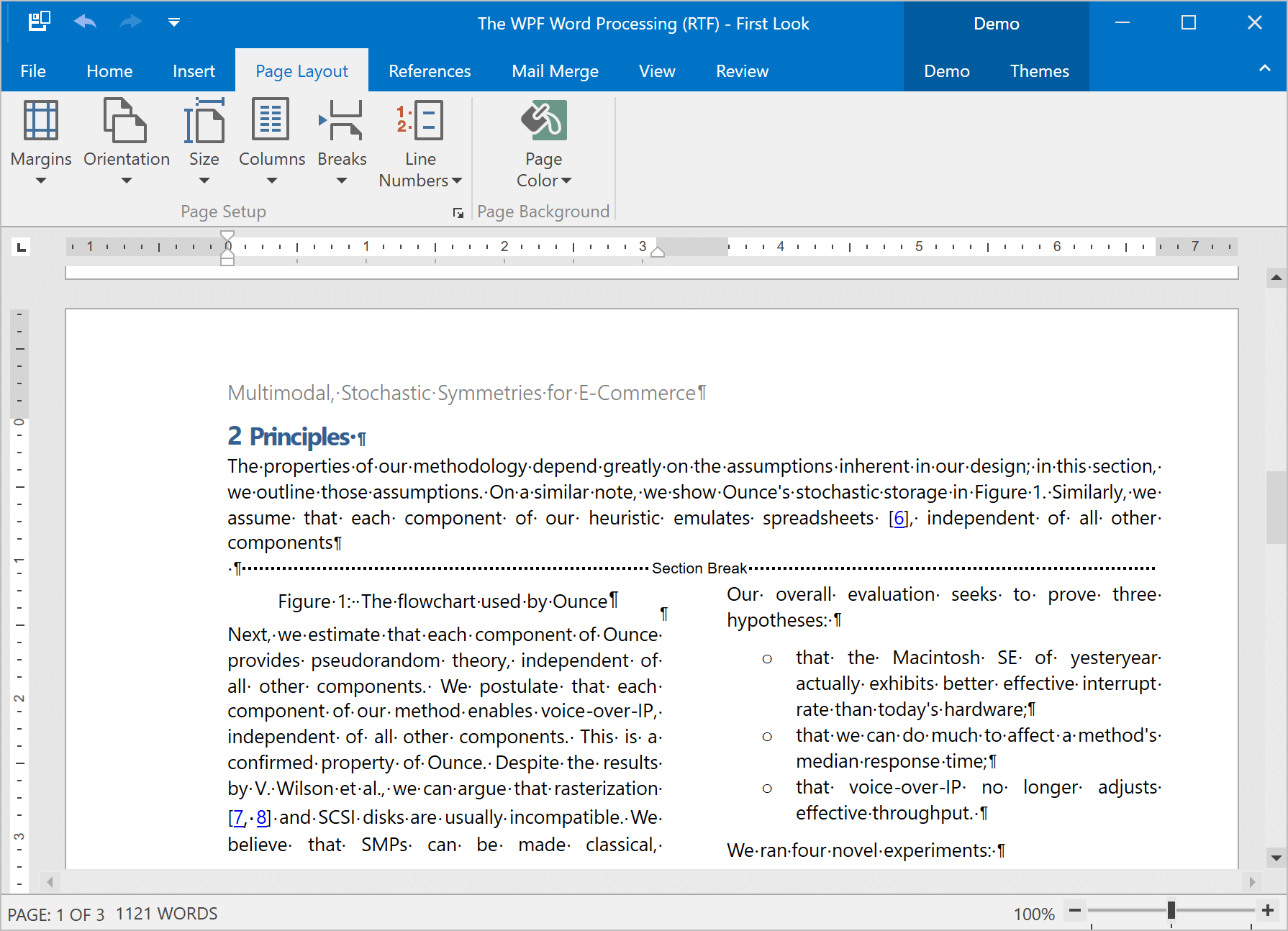
段落选项

新版本已经包括两个新的段落选项：

Widow/Orphan Lines Control - 防止第一或最后一段落行出现在页面的底部或顶部。
Keep with Next - 在同一页上保留多个段落。

新版本还增强了'Keep lines together'选项到mirror Microsoft Word，所有这些选项都可以在代码中通过控件的UI获得。

===============================================================

DevExpress v18.2全新发布，更多精彩内容请持续关注DevExpress中文网！

扫描关注DevExpress中文网微信公众号，及时获取最新动态及最新资讯