【LeetCode每天一题】Longest Common Prefix（最长前缀）

Write a function to find the longest common prefix string amongst an array of strings. If there is no common prefix, return an empty string "".

Example 1:            Input: ["flower","flow","flight"]                    Output: "fl"

Example 2:            Input: ["dog","racecar","car"]                     Output: ""                                  Explanation: There is no common prefix among the input strings.

Note:  All given inputs are in lowercase letters a-z.

思路

---

　　在看到这道题的时候我选择的是直接进行查找。从第一个字符串中提取出一个字符然后对每一个字符串相应位置进行比较。如果不先等直接返回结果。相等则继续向一下一位查找。时间复杂度为O(s*n)(s为最短字符串的长度， n为列表的长度)， 空间复杂度为O(s)。

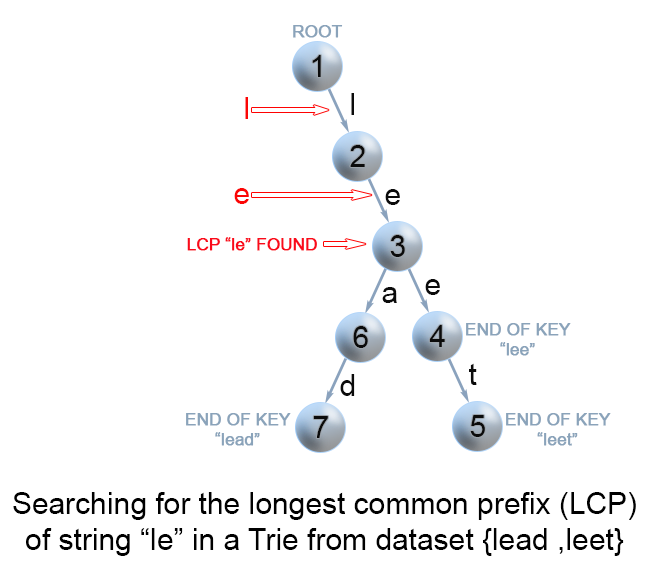
　　第二种办法是使用字典树来解决，但是需要我们先对列表中的字符串进行构造成字典树，最后从字典树的根节点进行查找当有分支的时候就停止。时间复杂度为O(x)（x是列表中所有字符串长度之和）, 时间复杂度为O(y)（字典树的大小）。

图示

---

第一种解法图示

第二种解法的图示

代码

---

 class Solution(object):
     def longestCommonPrefix(self, strs):
         """
         :type strs: List[str]
         :rtype: str
         """
         if len(strs) < :      # 长度小于2直接返回
             return strs[] if strs else ''

         res_str, min_len = '', len(min(strs))     # 设计结果返回量和最短的字符串长度
         i =
         while i < min_len:                        # 从小标第一个开始
             tem = strs[][i]                       # 取出第一个比较
             for j in strs:                        # 从第列表中第一个开始遍历
                 if j[i] != tem:                   # 如果不相等直接返回
                     return res_str
             res_str +=  tem
             i +=
         return res_str