八皇后问题 递归实现 C语言 超详细 思路 基础

八皇后问题 ：假设 將八个皇后放到国际象棋盘上，使其两两之间无法相互攻击。共有几种摆法？

基础知识：

国际象棋里，棋盘为8X8格。

皇后每步可以沿直线、斜线 走任意格。

思路：

1.想把8个皇后放进去，肯定最终每行只有一个皇后，每列只有一个皇后。

2.设个二维数组chess [ i ] [ j ] 模拟棋盘，cas存放摆法。i j 是表示i行j列：

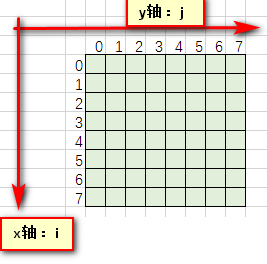
写一个用于递归的函数，思路如下

3.从上往下一行行的放皇后，放下一行时从最左边（第0列）放起，如果不能放就往右挪一格再试。注意判断右边有没有越界出棋盘。

4.写一个函数专门判断当前位置能不能放，只需要判断该位置的横、竖、两对角线，这四条线上有没有其他皇后即可。命名为check。

5.如果把最后一行放完了，那就统计上这个摆法，cas++。摆完最后一行不能继续判断下一行了。

6.放完一种情况，还要探究其他情况，可以把现在放好的皇后“拿走”，然后再试探 之前没试探过的棋盘格。

7.拿走皇后操作可以和不能放皇后的操作用同样的代码实现：

如果这个位置不能放，要把它置零，表示没有皇后。

如果这位置能放，那就放皇后（置1）。等一种情况讨论完，还得把它拿开，“拿开”也是置零的操作。

所以应该想办法排列上述代码，保证已经把摆出的情况记录下来，之后执行“拿开皇后”代码。

下面是递归函数部分：

void queen(int i,int j){
if(j>=line){ //如果右侧越界
 return ;
}

    if(check(i,j)==1){//如果能放
    chess[i][j]=1;//放皇后
	 if(i==line-1){//如果是最后一行，记录情况
	 cas++;
	 }
	 else{
	 queen(i+1,0);//不是最后一行就分析下一行
 	}
    }
	//下面这两句是最精彩的
 chess[i][j]=0;//如果此位置不能放，就置空（0），判断旁边的格子。
//如果此位置能放，走到这里就意味着上面的代码全部执行了，把皇后拿走（置零），再讨论其他情况，拿旁边位置试探。
 queen(i,j+1);
}

然后开始写判断函数check。需要判断的是8个方向，把它看成4条直线考虑。对于所在的横行，竖列，直接用for循环判断。接下来考虑对角线（红色）。

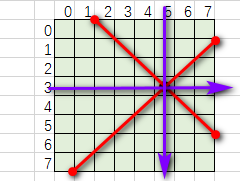
这样可以看出来，要判断的对角线是每个象限的平分线，每次 i ，j 的变化量是相等的，只是符号有差异。横纵坐标变化量的范围是-8~8，当对角线走到边框时停止判断。

为什么是-8到8呢？因为咱们没必要确定对角线的精确范围，上图是最理想的对角线，但是因为目标位置不同，对角线范围也不同，每次计算两端点是不可取的。

直接按最长对角线划：

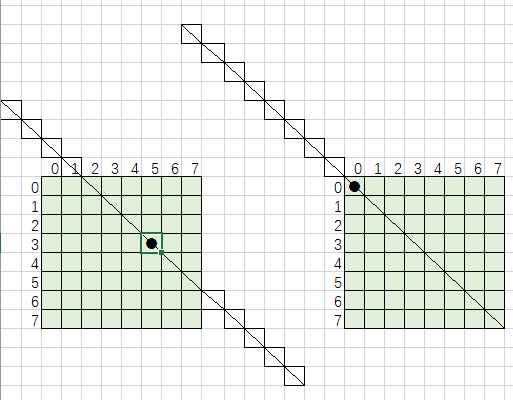
核心代码：

for(k=-line;k<=line;k++){//两对角线
 if(i+k>=0&&i+k<line&&j+k>=0&&j+k<line)//从左上到右下对角线，如果在棋盘格里
 if(chess[i+k][j+k]==1) return 0;

if(i-k>=0&&i-k<line&&j+k>=0&&j+k<line)//从左下到右上对角线，如果在棋盘格里
 if(chess[i-k][j+k]==1) return 0;
}

这个判断函数不重要，你写的函数达到目的就行。

注意一点，此函数只能设计成判断功能，不可以改变棋盘格的填充。

我刚开始觉得，当放置完上一个皇后，直接把这皇后所在的横纵斜方向全部填充一个数字，列为‘‘禁地’’，下一皇后放置时只要看待放入位置是否是“禁地”即可。但这么做是错的，因为不是把棋盘格填好一次就ok了，摆好一次后还需要把最后放的棋子拿开，探讨其他情况。如果划分禁地后，拿走皇后还得把禁地复原了，很麻烦的说。。而且代码量也不节省，就这么判断就行。

代码块的思路讲完，下面是完整代码。运行结果：92.

你写的程序也要保证这个结果。

#include<stdio.h>
#define line 8
void queen(int i,int j);
int check(int i,int j);
int chess[line][line];
int cas=0;
int xx,yy;

int main(){
queen(0,0);
printf("%d\n",cas);
return 0;
}

void queen(int i,int j){
if(j>=line){
return ;
}

if(check(i,j)==1){//如果能放
 chess[i][j]=1;//放皇后
 if(i==line-1){//如果是最后一行，记录情况
 cas++;
    /*下面是输出每种棋盘结果，供测试    

for (xx=0;xx<8;xx++)

for(yy=0;yy<8;yy++){

printf("%d",chess[xx][yy]);

if(yy==7)

printf("\n");

}

printf("\n");

上面是输出结果*/

}
else{
queen(i+1,0);//不是最后一行就分析下一行
 }
}
chess[i][j]=0;//如果此位置不能放，就置空（0），判断旁边的格子。
 //如果此位置能放，走到这里就意味着上面的代码全部执行了，把皇后拿走（置零），再讨论其他情况，拿旁边位置试探。
 queen(i,j+1);
}


int check(int i,int j){
int k;

for(k=0;k<line;k++){
if(chess[i][k]==1) return 0;//0=不能放
 }
for(k=0;k<line;k++){
if(chess[k][j]==1) return 0;
}
for(k=-line;k<=line;k++){//两对角线
 if(i+k>=0&&i+k<line&&j+k>=0&&j+k<line)//从左上到右下对角线
 if(chess[i+k][j+k]==1) return 0;

if(i-k>=0&&i-k<line&&j+k>=0&&j+k<line)//从左下到右上对角线
 if(chess[i-k][j+k]==1) return 0;
}
return 1;
}