opencv3.1线性可分svm例子及函数分析

https://www.cnblogs.com/qinguoyi/p/7272218.html

//摘自：http://docs.opencv.org/2.4/doc/tutorials/ml/introduction_to_svm/introduction_to_svm.html
#include <opencv2/core/core.hpp>
#include <opencv2/highgui/highgui.hpp>
#include <opencv2/ml/ml.hpp>
#include <iostream>

using namespace cv;
using namespace cv::ml;

int main()
{
    // Data for visual representation
    int width = 512, height = 512;
    Mat image = Mat::zeros(height, width, CV_8UC3);

    // Set up training data
    int labels[4] = { 1, -1, -1, -1};
    Mat labelsMat(4, 1, CV_32SC1, labels); //将labels转换成4行1列的32位单通道字符型阵列

    float trainingData[4][2] = { { 501, 10 }, { 255, 10 }, { 501, 255 }, { 10, 501 } };
    Mat trainingDataMat(4, 2, CV_32FC1, trainingData);//将训练数据转换成4行2列的32位单通道浮点型阵列

    // Set up SVM's parameters
    Ptr<SVM> svm = SVM::create();//建立一个空的svm文件
    svm->setType(SVM::Types::C_SVC);
    svm->setKernel(SVM::KernelTypes::LINEAR);
    svm->setTermCriteria (cvTermCriteria(CV_TERMCRIT_ITER, 100, 1e-6));//SVM的迭代训练过程的中止条件

    // Train the SVM
    svm->StatModel::train(trainingDataMat, SampleTypes::ROW_SAMPLE, labelsMat);

    Vec3b green(0, 255, 0), blue(255, 0, 0);
    // Show the decision regions given by the SVM
    for (int i = 0; i < image.rows; ++i)
    {
        for (int j = 0; j < image.cols; ++j)
    {
        Mat sampleMat = (Mat_<float>(1, 2) << j,i);//将每个i, j按照顺序输入进Mat
        float response = svm->predict(sampleMat);
        //std::cout << sampleMat << std::endl;
        //std::cout << response << std::endl;
        if (response == 1)
            image.at<Vec3b>(i,j) = green;
        else if (response == -1)
            image.at<Vec3b>(i,j) = blue;
        //std::cout << image.at<Vec3b>(i, j) << std::endl;
    }
    }
    imshow("SVM Simple Example", image); // show it to the user
    waitKey(0);
    std::cout << "done" << std::endl;
}

opencv3.1属于阉割版的opencv，很多以前的函数被改版，甚至删除掉，比如circle函数。

Mat初始化

Mat sampleMat = (Mat_<float>(1, 2) << j,i);是Mat的一种初始化方式，将每次循环的i，j输入进Mat，然后初始化。

.at<Vec3b>(i,j)

image.at<Vec3b>(i,j)，.at(int y, int x)表示用来存取图像中对应坐标为(x, y)的元素坐标，<type>为类型。Vec3b表示三通道的赋值类型。

Vec3b green(0, 255, 0)，也可以 Vec3b green;green[0]=0;green[1]=255;green[2]=0。

构造函数的参数(一共10个)：

<1>svm_type:指定SVM的类型(5种)：

• SVM::C_SVC : C类支持向量分类机。 n类分组  (n≥2)，允许用异常值惩罚因子C进行不完全分类。
• SVM::NU_SVC : 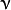类支持向量分类机。n类似然不完全分类的分类器。参数为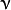取代C（其值在区间【0，1】中，nu越大，决策边界越平滑）。
• SVM::ONE_CLASS : 单分类器，所有的训练数据提取自同一个类里，然后SVM建立了一个分界线以分割该类在特征空间中所占区域和其它类在特征空间中所占区域。
• SVM::EPS_SVR : 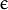类支持向量回归机。训练集中的特征向量和拟合出来的超平面的距离需要小于p。异常值惩罚因子C被采用。
• SVM::NU_SVR : 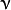类支持向量回归机。 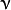代替了 p。

<2>kernel_type:SVM的内核类型(4种)：

• SVM::LINEAR : 线性内核，没有任何向映射至高维空间，线性区分（或回归）在原始特征空间中被完成，这是最快的选择。

            .

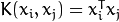• SVM::POLY : 多项式内核：

             .

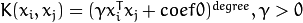• SVM::RBF : 基于径向的函数，对于大多数情况都是一个较好的选择：

             .

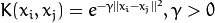• SVM::SIGMOID : Sigmoid函数内核：

            .

<3>degree:内核函数（POLY）的参数degree。

<4>gamma:内核函数（POLY/ RBF/ SIGMOID）的参数。

<5>coef0:内核函数（POLY/ SIGMOID）的参数coef0。

<6>Cvalue:SVM类型（C_SVC/ EPS_SVR/ NU_SVR）的参数C。

<7>nu:SVM类型（NU_SVC/ ONE_CLASS/ NU_SVR）的参数 。

<8>p:SVM类型（EPS_SVR）的参数。

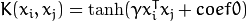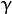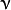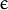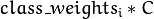<9>class_weights:C_SVC中的可选权重，赋给指定的类，乘以C以后变成 。所以这些权重影响不同类别的错误分类惩罚项。权重越大，某一类别的误分类数据的惩罚项就越大。

<10>term_crit:SVM的迭代训练过程的中止条件，解决部分受约束二次最优问题。您可以指定的公差和/或最大迭代次数。

CvTermCriteria  

迭代算法的终止准则

#define CV_TERMCRIT_ITER    1

#define CV_TERMCRIT_NUMBER  CV_TERMCRIT_ITER

#define CV_TERMCRIT_EPS     2

typedef struct CvTermCriteria  {

int    type;  /* CV_TERMCRIT_ITER 和CV_TERMCRIT_EPS二值之一，或者二者的组合 */

int    max_iter; /* 最大迭代次数 */

double epsilon; /* 结果的精确性 */

}

CvTermCriteria;

/* 构造函数 */

inline  CvTermCriteria  cvTermCriteria( int type, int max_iter, double epsilon );

PS:OpenCV2.x的版本中，SVM还有Parameters参数，更新到3.x版本后就取消了，改为如下图的set函数：

 svm->setType(SVM::Types::C_SVC);
 svm->setKernel(SVM::KernelTypes::LINEAR);
 svm->setTermCriteria (cvTermCriteria(CV_TERMCRIT_ITER, 100, 1e-6));//100是迭代次数，1e-6是精确度。

上面的3-9都是有使用条件的，比如LINEAR为内核的时候，3-9都是不需要的,设置完如上代码后可以直接训练，也可以调用自动训练函数，那样的话其实意义不大：

svm->StatModel::train(trainingDataMat, SampleTypes::ROW_SAMPLE, labelsMat);

当我们选择另外三个内核的时候，需要对3-9分别进行设置，设置后可以进行直接训练：

svm_ = cv::ml::SVM::create();
    svm_->setType(cv::ml::SVM::C_SVC);
    svm_->setKernel(cv::ml::SVM::RBF);
    svm_->setDegree(0.1);
    // 1.4 bug fix: old 1.4 ver gamma is 1  //1.4版本bug修复
    svm_->setGamma(1);
    svm_->setCoef0(0.1);
    svm_->setC(1);
    svm_->setNu(0.1);
    svm_->setP(0.1);
    svm_->setTermCriteria(cvTermCriteria(CV_TERMCRIT_ITER, 20000, 0.0001));
　　svm_->train(train_data);

也可以进行自动训练trainAuto（）函数

Ptr<cv::ml::TrainData>tdata;    //将训练数据和标签整合成tdata
    tdata = TrainData::create(trainingDataMat, cv::ml::SampleTypes::ROW_SAMPLE, labelsMat);
    svm->trainAuto(tdata, 10,
        SVM::getDefaultGrid(SVM::C),
        SVM::getDefaultGrid(SVM::GAMMA),
        SVM::getDefaultGrid(SVM::P),
        SVM::getDefaultGrid(SVM::NU),
        SVM::getDefaultGrid(SVM::COEF),
        SVM::getDefaultGrid(SVM::DEGREE),
        true);

• k_fold: 交叉验证参数。训练集被分成k_fold的自子集。其中一个子集是用来测试模型，其他子集则成为训练集。所以，SVM算法复杂度是执行k_fold的次数。
• *Grid: (6个)对应的SVM迭代网格参数。
• balanced: 如果是true则这是一个2类分类问题。这将会创建更多的平衡交叉验证子集。

训练完成后保存txt或者xml文件：

svm->save("svm_image.xml");

OpenCV3.1中载入模型的语句：

//Ptr<SVM> svmp = SVM::create();
//svmp = SVM::load<SVM>("svm_image.xml");
Ptr<SVM> svmp =  SVM::load<SVM>("svm_image.xml");

载入之后就可以进行预测了：

//返回的是预测数据距离决策面（超平面）的几何距离
float response = svmp->predict(sampleMat, noArray(), StatModel::Flags::RAW_OUTPUT);

//返回的是标签分类
float response = svmp->predict(sampleMat, noArray(), 0);
float response = svmp->predict(sampleMat);