10.25 正睿停课训练 Day9

目录

• 2018.10.25 正睿停课训练 Day9
  • A 数独(思路 DP)
  • B 红绿灯(最短路Dijkstra)
  • C 轰炸(计算几何 圆并)
  • 考试代码
    • B
    • C

---

2018.10.25 正睿停课训练 Day9

期望得分：100+60+20

实际得分：100+0+0

比赛链接

Dijkstra模板题爆零了。我还有救吗

A 数独(思路 DP)

题目链接

先是想到，限制的是1，但其实在数独里1和2,3,...,9别的数没啥特殊的地方啊，可以忽略其它数的种类？

好，上面这句话没什么用。

考虑到每种合法的填1方案（不考虑其它数，先只填1），对数独的解数的贡献是一样的。

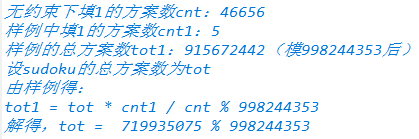
所以我们求 \(当前填1合法方案数/无限制填1合法方案数\) 这个比例，再乘以无限制的数独总解数就行了。

当前填1合法方案数可以DP，状压一下，三行三行转移，非常轻松。直接DFS也随便过。

数独总解数大概可以各种剪枝+优化（对称性）在本机跑出来。反正我选择百度。

---

搜索求解的数量（orz wph）：

---

或者面向样例得到解的数量（orz wzh）

---

//49ms	504kb
#include <cstdio>
#include <cctype>
#include <cstring>
#include <algorithm>
//#define gc() getchar()
#define MAXIN 100000
#define gc() (SS==TT&&(TT=(SS=IN)+fread(IN,1,MAXIN,stdin),SS==TT)?EOF:*SS++)
#define mod 998244353
#define lb(x) (x&-(x))
#define Mod(x) x>=mod&&(x-=mod)
typedef long long LL;
const int N=12,M=(1<<9)+2;

int bit[M];
bool ban[N][N];
char IN[MAXIN],*SS=IN,*TT=IN;

inline int read()
{
	int now=0;register char c=gc();
	for(;!isdigit(c);c=gc());
	for(;isdigit(c);now=now*10+c-'0',c=gc());
	return now;
}
inline LL Read()
{
	LL now=0;register char c=gc();
	for(;!isdigit(c);c=gc());
	for(;isdigit(c);now=now*10+c-'0',now%=mod,c=gc());
	return now;
}
inline int FP(int x,int k)
{
	int t=1;
	for(; k; k>>=1,x=1ll*x*x%mod)
		if(k&1) t=1ll*t*x%mod;
	return t;
}
inline bool Check(int a,int b)
{
	if(a<3) return b>=3;
	if(a>5) return b<=5;
	return b<=2||b>=6;
}
int Calc()
{
	static int f[M];
	memset(f,0,sizeof f);
	f[0]=1;
	int all=(1<<9)-1;
	for(int s=0; s<all; ++s)
	{
		int cnt=bit[s];
		if(cnt%3) continue;
		for(int a=0; a<9; ++a)
			if(!(s>>a&1)&&!ban[cnt+1][a+1])
				for(int b=0; b<9; ++b)
					if(!(s>>b&1)&&!ban[cnt+2][b+1]&&Check(a,b))
						for(int c=0; c<9; ++c)
						{
							if(s>>c&1||ban[cnt+3][c+1]||!Check(a,c)||!Check(b,c)) continue;
							int ss=s|(1<<a)|(1<<b)|(1<<c);
							f[ss]+=f[s], Mod(f[ss]);
						}
	}
	return f[all];
}

int main()
{
	const int Sum=719935075;//Read(); //6670903752021072936960
	const int tot=46656,inv=549081465;// int tot=Calc(),inv=FP(tot,mod-2);
	for(int i=1; i<M; ++i) bit[i]=bit[i^lb(i)]+1;
	for(int T=read(); T--; )
	{
		for(int i=1; i<=9; ++i)
		{
			register char c=gc(); for(;c!='0'&&c!='1';c=gc());
			ban[i][1]=c=='1';
			for(int j=2; j<=9; ++j) ban[i][j]=gc()=='1';
		}
		int now=Calc();
		printf("%d\n",(int)(1ll*Sum*now%mod*inv%mod));
	}
	return 0;
}

B 红绿灯(最短路Dijkstra)

题目链接

不管一条边怎么样，我们到达一个点时肯定是越早越好啊（不会更差）。

所以直接Dijkstra就行了。边权就模拟一下。

//2762ms	54532kb
#include <queue>
#include <cstdio>
#include <cctype>
#include <cstring>
#include <algorithm>
#define mp std::make_pair
#define pr std::pair<LL,int>
//#define gc() getchar()
#define MAXIN 300000
#define gc() (SS==TT&&(TT=(SS=IN)+fread(IN,1,MAXIN,stdin),SS==TT)?EOF:*SS++)
typedef int LL;//longlong?
const int N=5e5+6,M=2e6+7;

int Enum,H[N],nxt[M],to[M],len[M],K[M],L[M],R[M];
char IN[MAXIN],*SS=IN,*TT=IN;

inline int read()
{
	int now=0;register char c=gc();
	for(;!isdigit(c);c=gc());
	for(;isdigit(c);now=now*10+c-'0',c=gc());
	return now;
}
inline void AE(int r,int l,int k,int d,int v,int u)
{
	to[++Enum]=v, nxt[Enum]=H[u], H[u]=Enum, len[Enum]=d, K[Enum]=k, L[Enum]=l, R[Enum]=r;
	to[++Enum]=u, nxt[Enum]=H[v], H[v]=Enum, len[Enum]=d, K[Enum]=k, L[Enum]=l, R[Enum]=r;
}
inline int Calc(int now,int d,int k,int l,int r)
{
	int tm=0;
	if(now>r) tm+=k-now+l;
	else if(now<l) tm+=l-now;
	else if(r-now+1>=d) return d;
	else d-=r-now+1, tm+=k-now+l;
	now=(d-1)/(r-l+1), tm+=now*k, d-=now*(r-l+1);//(d-1)/len not d/len!
	return tm+d;
}
void Dijkstra(int n)
{
	static LL dis[N];
	static bool vis[N];
	static std::priority_queue<pr> q;

	memset(dis,0x3f,sizeof dis);
	dis[1]=0, q.push(mp(0,1));
	while(!q.empty())
	{
		int x=q.top().second; q.pop();
		if(vis[x]) continue;
		vis[x]=1; LL ds=dis[x];
		for(int i=H[x],v,tm; i; i=nxt[i])
			if(tm=Calc(ds%K[i],len[i],K[i],L[i],R[i]),dis[v=to[i]]>ds+tm)
				q.push(mp(-(dis[v]=ds+tm),v));
	}
	for(int i=1; i<=n; ++i) printf("%d\n",dis[i]);
}

int main()
{
	Enum=1; int n=read(),m=read();
	for(int i=1; i<=m; ++i) AE(read(),read(),read(),read(),read(),read());
	Dijkstra(n);

	return 0;
}

C 轰炸(计算几何 圆并)

题目链接

求圆并，然后找覆盖\(k\)次的部分？

好不NOIP啊，咕了。

咕

考试代码

B

迷之全RE懒得调。

#include <queue>
#include <cstdio>
#include <cctype>
#include <cstring>
#include <algorithm>
//#define gc() getchar()
#define MAXIN 300000
#define gc() (SS==TT&&(TT=(SS=IN)+fread(IN,1,MAXIN,stdin),SS==TT)?EOF:*SS++)
#define Add(x,y) (x+y>=20?x+y-20:x+y)
typedef long long LL;
const int N=5e5+6,M=2e6+7;
const LL INF=0x3f3f3f3f3f3f3f3f;

int Enum,H[N],nxt[M],to[M],len[M],K[M],L[M],R[M],f[M>>1][20];
char IN[MAXIN],*SS=IN,*TT=IN;
struct Node
{
	LL ds; int x,tm;
	bool operator <(const Node &a)const
	{
		return ds>a.ds;
	}
};

inline int read()
{
	int now=0;register char c=gc();
	for(;!isdigit(c);c=gc());
	for(;isdigit(c);now=now*10+c-'0',c=gc());
	return now;
}
inline void AE(int r,int l,int k,int d,int v,int u)
{
	to[++Enum]=v, nxt[Enum]=H[u], H[u]=Enum, len[Enum]=d, K[Enum]=k, L[Enum]=l, R[Enum]=r;
	to[++Enum]=u, nxt[Enum]=H[v], H[v]=Enum, len[Enum]=d, K[Enum]=k, L[Enum]=l, R[Enum]=r;
	for(int i=0; i<k; ++i)
	{
		int tmp=i,tm=0,dd=d;
		if(tmp>r) tm+=l+k-tmp;
		else if(tmp<l) tm+=l-tmp;
		else if(tmp!=l)
		{
			if(r-tmp+1>=dd) {f[Enum>>1][i]=dd; continue;}
			else dd-=r-tmp+1, tm+=k-tmp+l;
		}
		tmp=dd/(r-l+1), tm+=tmp*k, dd-=tmp*(r-l+1);
		f[Enum>>1][i]=tm+dd;
	}
}
void Dijkstra(int n)
{
	static bool vis[N][20];
	static LL dis[N][20];
	static std::priority_queue<Node> q;
	memset(dis,0x3f,sizeof dis);
	dis[1][0]=0, q.push((Node){0,1,0});
	while(!q.empty())
	{
		Node tmp=q.top(); q.pop();
		LL ds=tmp.ds; int x=tmp.x, tm=tmp.tm;
		if(vis[x][tm]) continue;
		vis[x][tm]=1;
		for(int i=H[x],v,use,tmp; i; i=nxt[i])
		{
			v=to[i], use=f[i>>1][tm%K[i]], tmp=Add(tm,use);
			if(dis[v][tmp]<=ds+use) continue;
			q.push((Node){dis[v][tmp]=ds+use,v,tmp});
		}
	}
	for(int i=1; i<=n; ++i)
	{
		LL ans=INF;
		for(int j=0; j<20; ++j) ans=std::min(ans,dis[i][j]);
		printf("%lld\n",ans);
	}
}

int main()
{
//	freopen(".in","r",stdin);
//	freopen(".out","w",stdout);

	Enum=1; int n=read(),m=read();
	for(int i=1; i<=m; ++i) AE(read(),read(),read(),read(),read(),read());
	Dijkstra(n);

	return 0;
}

C

为啥输出0.0000没分啊 明明有理有据啊

#include <cstdio>
#include <cctype>
#include <algorithm>
#define gc() getchar()
typedef double db;
const int N=105;

int n,K,Lim;
struct Point
{
	int x,y,a;
}p[N];

inline int read()
{
	int now=0,f=1;register char c=gc();
	for(;!isdigit(c);c=='-'&&(f=-1),c=gc());
	for(;isdigit(c);now=now*10+c-'0',c=gc());
	return now*f;
}

int main()
{
//	freopen(".in","r",stdin);
//	freopen(".out","w",stdout);

	for(int T=read(); T--; )
	{
		n=read(),K=read(),Lim=read();
		for(int i=1; i<=n; ++i) p[i]=(Point){read(),read(),read()};
		if(K==1||1) printf("0.0000\n");
//		else if(!Lim && K==n) Subtask3::Main();
//		else if(!Lim) Subtask1::Main();

	}
	return 0;
}