图的遍历算法：DFS、BFS
DFS）和广度优先搜索（BFS）。DFS(深度优先搜索)算法
Depth-First-Search
深度优先算法，是一种用于遍历或搜索树或图的算法。沿着树的深度遍历树的节点，尽可能深的搜索树的分支。
当节点v的所在边都己被探寻过，搜索将回溯到发现节点v的那条边的起始节点。 这一过程一直进行到已发现从源节点可达的所有节点为止。
如果还存在未被发现的节点， 则选择其中一个作为源节点并重复以上过程，整个进程反复进行直到所有节点都被访问为止。属于盲目搜索。
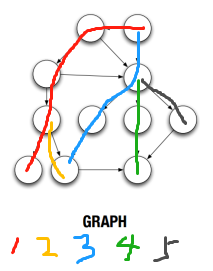
DFS可用堆栈(Stack)和递归(Recursive)两种方法实现
如何跟踪下一步搜索的位置?
使用Stack： 列表中只从一端添加和移除:
- Push：添加元素
- Pop：删除一个元素
如何跟踪访问过的内容?
HashSet:：常量添加，删除和搜索
如何跟踪从开始到目标的路径?
HashMap：将每个节点链接到发现它的节点
堆栈和递归实现过程（伪代码）：
BFS (广度优先搜索)算法
Breadth-First-Search
BFS是从根节点开始，沿着树的宽度遍历树的节点。
如果所有节点均被访问，则算法中止。 广度优先搜索的实现本篇笔记采用队列。
如何跟踪下一步搜索的位置?
Queue：列出你只从一端添加和移除的地方
- enqueue：添加一个元素
- deque：删除一个元素
如何跟踪访问过的内容?
HashSet：定时添加，删除和搜索
如何跟踪从开始到目标的路径?
HashMap：将每个节点链接到发现它的节点
和DFS唯一不同的是BFS使用队列来实现，伪代码如下：
学习参考资料：
【Python算法】遍历(Traversal)、深度优先(DFS)、广度优先(BFS)
搜索思想——DFS & BFS（基础基础篇）
图的遍历算法：DFS、BFS的更多相关文章
- 图的基本算法（BFS和DFS）
图是一种灵活的数据结构,一般作为一种模型用来定义对象之间的关系或联系.对象由顶点(V)表示,而对象之间的关系或者关联则通过图的边(E)来表示. 图可以分为有向图和无向图,一般用G=(V,E)来表示图. ...
- 数据结构（三十二）图的遍历（DFS、BFS）
图的遍历和树的遍历类似.图的遍历是指从图中的某个顶点出发,对图中的所有顶点访问且仅访问一次的过程.通常有两种遍历次序方案:深度优先遍历和广度优先遍历. 一.深度优先遍历 深度优先遍历(Depth_Fi ...
- 7.9模拟赛T1图的遍历（dfs）
图的遍历(dfs) [题目描述] 对于一个有向图G来说,我们存在一个经典的遍历算法,就是DFS (深度优先搜索遍历).将G以1号点为起点进行DFS后,我们可以 得到G的一棵DFS遍历树T.就此,我们可 ...
- 图的遍历：DFS和BFS
图的遍历一般由两者方式:深度优先搜索(DFS),广度优先搜索(BFS),深度优先就是先访问完最深层次的数据元素,而BFS其实就是层次遍历,每一层每一层的遍历. 1.深度优先搜索(DFS) 我一贯习惯有 ...
- 图的广度优先遍历算法（BFS）
在上一篇文章我们用java演示了图的数据结构以及图涉及到的深度优先遍历算法,本篇文章将继续演示图的广度优先遍历算法.广度优先遍历算法主要是采用了分层的思想进行数据搜索.其中也需要使用另外一种数据结构队 ...
- PAT Advanced A1021 Deepest Root (25) [图的遍历，DFS，计算连通分量的个数，BFS，并查集]
题目 A graph which is connected and acyclic can be considered a tree. The height of the tree depends o ...
- 图的两种遍历：DFS&BFS
DFS和BFS在图中的应用: 图连通性判定:路径的存在性:图中是否存在环:求图的最小生成树:求图的关键路径:求图的拓扑排序. DFS:简单的说,先一直往深处走,直到不能再深了,再从另一条路开始往深处走 ...
- 第七十五课 图的遍历（DFS）
添加DFS函数: #ifndef GRAPH_H #define GRAPH_H #include "Object.h" #include "SharedPointer. ...
- POJ-1469 COURSES ( 匈牙利算法 dfs + bfs )
题目链接: http://poj.org/problem?id=1469 Description Consider a group of N students and P courses. Each ...
随机推荐
- C++11 正则表达式——基础知识介绍
C++11开始支持正则表达式,使得处理文本更加简洁方便.C++11 支持六种正则表达式语法:ECMAScript, basic(POSIX Basic Regular Expressions), ex ...
- 我要搬家到csdn，大家到那里来看我吧，平台更大，看到的人更多！
ruby代码 #encoding: utf-8 require 'net/http' require 'open-uri' require 'nokogiri' # 用于解析html的模块 # sud ...
- ABAP 内表(internal table) 标题行(header line) 工作区(work area) 简介 - [SAP]
刚开始学ABAP的时候,学到iternal table时,感觉一阵混乱.搞不清楚什么是work area,什么是header line,以及occurs是干什么用的.今天终于差不多搞明白了(我还是太弱 ...
- java中自定义注释@interface的用法
一.什么是注释 说起注释,得先提一提什么是元数据(metadata).所谓元数据就是数据的数据.也就是说,元数据是描述数据的.就象数据表中的字段一样,每个字段描述了这个字段下的数据的含义.而J ...
- ODbgScript 2.01帮助文档
-------------------------------ODbgScript original pluginhttp://github.com/odbgscript--------------- ...
- 【转】使用Log4Net进行日志记录
首先说说为什么要进行日志记录.在一个完整的程序系统里面,日志系统是一个非常重要的功能组成部分.它可以记录下系统所产生的所有行为,并按照某种规范表达出来.我们可以使用日志系统所记录的信息为系统进行排错, ...
- Spark学习笔记——基于MLlib的机器学习
使用MLlib库中的机器学习算法对垃圾邮件进行分类 分类的垃圾邮件的如图中分成4个文件夹,两个文件夹是训练集合,两个文件夹是测试集合 build.sbt文件 name := "spark-f ...
- Java Annotation 应用 -- 导出Excel表格
相关知识链接: Introspector(内省) POI 1.声明注解 package com.ciic.component.excel; import java.lang.annotation.El ...
- 排序算法--选择排序(Selection Sort)_C#程序实现
排序算法--选择排序(Selection Sort)_C#程序实现 排序(Sort)是计算机程序设计中的一种重要操作,也是日常生活中经常遇到的问题.例如,字典中的单词是以字母的顺序排列,否则,使用起来 ...
- 如何用VBA实现格式刷的功能？
1. http://club.excelhome.net/thread-373686-1-1.html 复制1格式Selection.CopyFormat粘贴格式Selection.PasteForm ...