[LeetCode] 43. Multiply Strings ☆☆☆(字符串相乘)

字符串乘法

转载：43. Multiply Strings

题目描述

就是两个数相乘，输出结果，只不过数字很大很大，都是用 String 存储的。也就是传说中的大数相乘。

解法一

我们就模仿我们在纸上做乘法的过程写出一个算法。

个位乘个位，得出一个数，然后个位乘十位，全部乘完以后，就再用十位乘以各个位。然后百位乘以各个位，最后将每次得出的数相加。十位的结果要补 1 个 0 ，百位的结果要补两个 0 。相加的话我们可以直接用之前的大数相加。直接看代码吧。

public String multiply(String num1, String num2) {
    if (num1.equals("0") || num2.equals("0")) {
        return "0";
    }
    String ans = "0";
    int index = 0; //记录当前是哪一位，便于后边补 0
    for (int i = num2.length() - 1; i >= 0; i--) {
        int carry = 0; //保存进位
        String ans_part = ""; //直接用字符串保存每位乘出来的数
        int m = num2.charAt(i) - '0';
        //乘上每一位
        for (int j = num1.length() - 1; j >= 0; j--) {
            int n = num1.charAt(j) - '0';
            int mul = m * n + carry;
            ans_part = mul % 10 + "" + ans_part;
            carry = mul / 10;
        }
        if (carry > 0) {
            ans_part = carry + "" + ans_part;
        }
        //补 0
        for (int k = 0; k < index; k++) {
            ans_part = ans_part + "0";
        }
        index++;
        //和之前的结果相加
        ans = sumString(ans, ans_part);
    }
    return ans;
}
//大数相加
private String sumString(String num1, String num2) {
    int carry = 0;
    int num1_index = num1.length() - 1;
    int num2_index = num2.length() - 1;
    String ans = "";
    while (num1_index >= 0 || num2_index >= 0) {
        int n1 = num1_index >= 0 ? num1.charAt(num1_index) - '0' : 0;
        int n2 = num2_index >= 0 ? num2.charAt(num2_index) - '0' : 0;
        int sum = n1 + n2 + carry;
        carry = sum / 10;
        ans = sum % 10 + "" + ans;
        num1_index--;
        num2_index--;
    }
    if (carry > 0) {
        ans = carry + "" + ans;
    }
    return ans;
}

时间复杂度：O（m * n）。m，n 是两个字符串的长度。

空间复杂度：O（1）。

解法二

参考这里。

上边的解法非常简单粗暴，但是不够优雅。我们看一下从未见过的一种竖式计算。

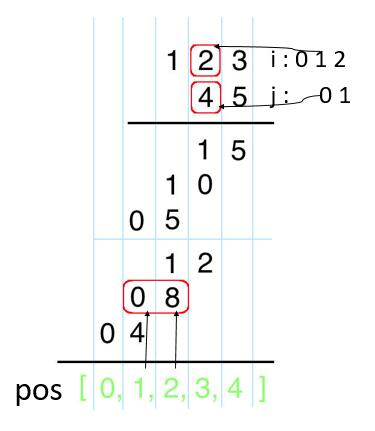
我们把进位先不算，写到对应的位置。最后再统一更新 pos 中的每一位。

而对于运算中的每个结果，可以观察出一个结论。

num1 的第 i 位乘上 num2 的第 j 位，结果会分别对应 pos 的第 i + j 位和第 i + j + 1 位。

例如图中的红色部分，num1 的第 1 位乘上 num2 的第 0 位，结果就对应 pos 的第 1 + 0 = 1 和 1 + 0 + 1 = 2 位。

有了这一点，我们就可以遍历求出每一个结果，然后更新 pos 上的值就够了。

public String multiply(String num1, String num2) {
    if (num1.equals("0") || num2.equals("0")) {
        return "0";
    }
    int n1 = num1.length();
    int n2 = num2.length();
    int[] pos = new int[n1 + n2]; //保存最后的结果
    for (int i = n1 - 1; i >= 0; i--) {
        for (int j = n2 - 1; j >= 0; j--) {
            //相乘的结果
            int mul = (num1.charAt(i) - '0') * (num2.charAt(j) - '0');
            //加上 pos[i+j+1] 之前已经累加的结果
            int sum = mul + pos[i + j + 1];
            //更新 pos[i + j]
            pos[i + j] += sum / 10;
            //更新 pos[i + j + 1]
            pos[i + j + 1] = sum % 10;
        }
    }
    StringBuilder sb = new StringBuilder();
    for (int i = 0; i < pos.length; i++) {
        //判断最高位是不是 0
        if (i == 0 && pos[i] == 0) {
            continue;
        }
        sb.append(pos[i]);
    }
    return sb.toString();
}

时间复杂度：O（m * n）。m，n 是两个字符串的长度。

空间复杂度：O（m + n）。m，n 是两个字符串的长度。

解法三(me) 完全模拟乘法进位

public String multiply(String ss, String tt) {
        if (null == ss || ss.length() <=  || null == tt || tt.length() <= ) {
            return null;
        }
        if (ss.equals("") || tt.equals("")) {
            return "";
        }
        int ssLen = ss.length();
        int ttLen = tt.length();
        int[] res = new int[ssLen + ttLen];//用数组存不用long，是为了防止数字越界
        int startIndex = ;//最低位开始的index，确定是10^startIndex 的多少倍值
        for (int i = ssLen - ; i >= ; i--) {
            int oldStartIndex = startIndex;
            int iNum = Integer.parseInt(String.valueOf(ss.charAt(i)));
            for (int k = ttLen - ; k >= ; k--) {
                int kNum = Integer.parseInt(String.valueOf(tt.charAt(k)));
                int curNum = iNum * kNum;
                res[startIndex] += curNum % ;
                if (res[startIndex] >= ) {//进位
                    res[startIndex] = res[startIndex] % ;
                    res[startIndex + ] += ;
                }
                res[startIndex + ] += curNum / ;
                if (res[startIndex + ] >= ) {//进位
                    res[startIndex + ] = res[startIndex + ] % ;
                    res[startIndex + ] += ;
                }
                startIndex++;
            }
            startIndex = oldStartIndex + ;
        }
        StringBuilder sb = new StringBuilder();
        boolean isStart0 = false;//去掉最高位的0
        for (int i = res.length - ; i >= ; i--) {
            if (res[i] !=  || isStart0) {
                sb.append(res[i]);
                isStart0 = true;
            }

        }
        return sb.toString();
    }