Deep Learning基础--word2vec 中的数学原理详解

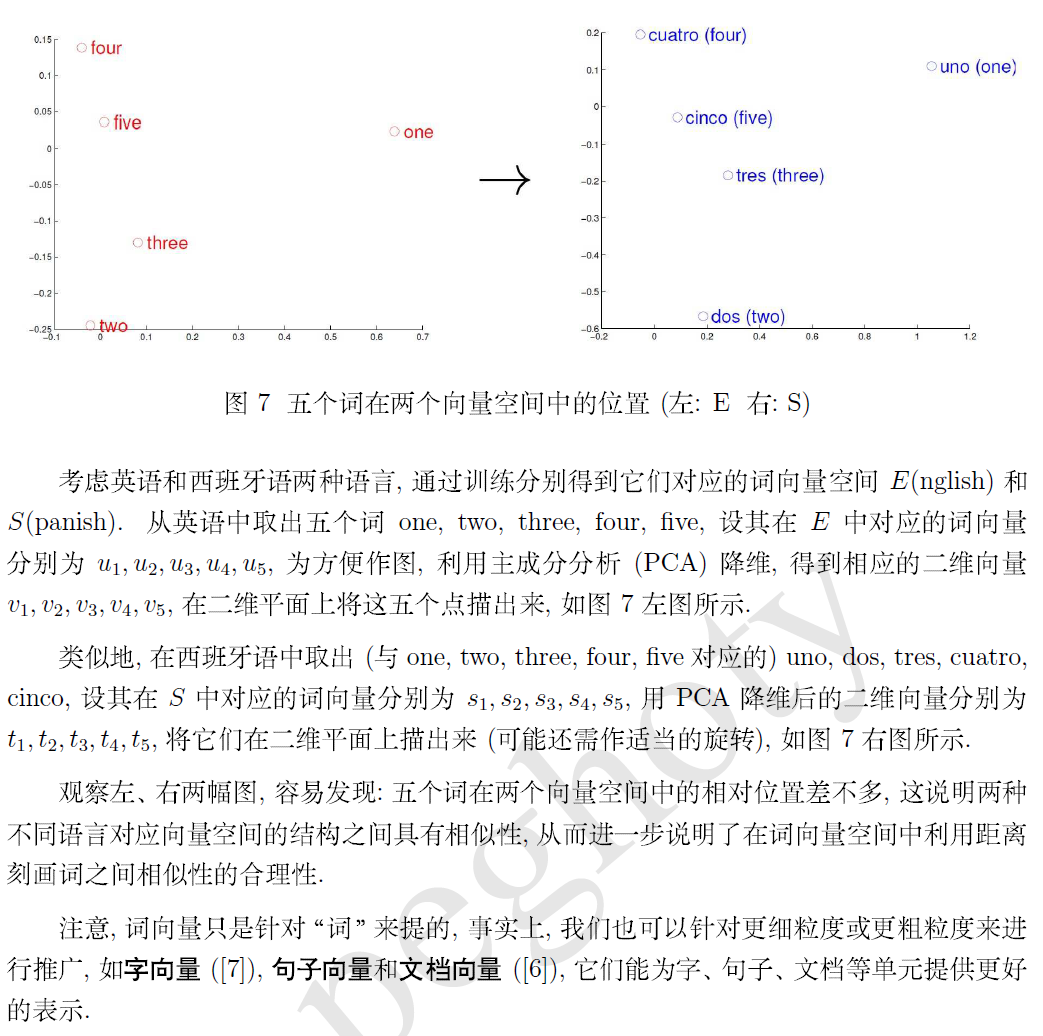
word2vec 是 Google 于 2013 年开源推出的一个用于获取 word vector 的工具包，它简单、高效，因此引起了很多人的关注。由于 word2vec 的作者 Tomas Mikolov 在两篇相关的论文 [3,4] 中并没有谈及太多算法细节，因而在一定程度上增加了这个工具包的神秘感。一些按捺不住的人于是选择了通过解剖源代码的方式来一窥究竟，出于好奇，我也成为了他们中的一员。读完代码后，觉得收获颇多，整理成文，给有需要的朋友参考。

目录

（一）目录和前言
（二）预备知识
（三）背景知识
（四）基于 Hierarchical Softmax 的模型
（五）基于 Negative Sampling 的模型
（六）若干源码细节

作者: peghoty 

出处: http://blog.csdn.net/itplus/article/details/37999613

欢迎转载/分享, 但请务必声明文章出处.