洛谷P2047 [NOI2007]社交网络 [图论，最短路计数]

　　题目传送门

社交网络

题目描述

在社交网络（social network）的研究中，我们常常使用图论概念去解释一些社会现象。不妨看这样的一个问题。在一个社交圈子里有n个人，人与人之间有不同程度的关系。我 们将这个关系网络对应到一个n个结点的无向图上，两个不同的人若互相认识，则在他们对应的结点之间连接一条无向边，并附上一个正数权值c，c越小，表示两 个人之间的关系越密切。

我们可以用对应结点之间的最短路长度来衡量两个人s和t之间的关系密切程度，注意到最短路径上的其他结点为s和t的联系提供了某种便利， 即这些结点对于s 和t之间的联系有一定的重要程度。我们可以通过统计经过一个结点v的最短路径的数目来衡量该结点在社交网络中的重要程度。

考虑到两个结点A和B之间可能会有多条最短路径。我们修改重要程度的定义如下：

令Cs,t表示从s到t的不同的最短路的数目，Cs,t(v)表示经过v从s到t的最短路的数目；则定义

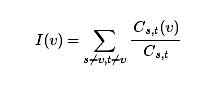
为结点v在社交网络中的重要程度。

为了使I(v)和Cs,t(v)有意义，我们规定需要处理的社交网络都是连通的无向图，即任意两个结点之间都有一条有限长度的最短路径。

现在给出这样一幅描述社交网络s的加权无向图，请你求出每一个结点的重要程度。

输入输出格式

输入格式：

输入第一行有两个整数，n和m，表示社交网络中结点和无向边的数目。在无向图中，我们将所有结点从1到n进行编号。

接下来m行，每行用三个整数a, b, c描述一条连接结点a和b，权值为c的无向边。注意任意两个结点之间最多有一条无向边相连，无向图中也不会出现自环（即不存在一条无向边的两个端点是相同的结点）。

输出格式：

输出包括n行，每行一个实数，精确到小数点后3位。第i行的实数表示结点i在社交网络中的重要程度。

输入输出样例

输入样例#1：

4 4
1 2 1
2 3 1
3 4 1
4 1 1

输出样例#1：

1.000
1.000
1.000
1.000

说明

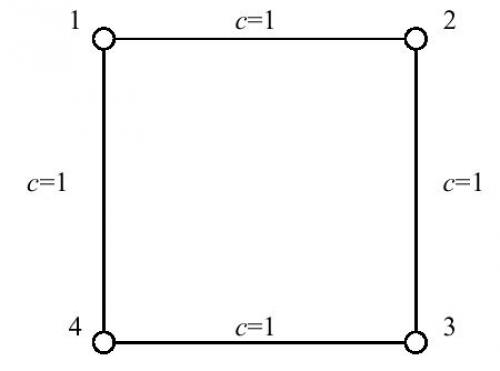
对于1号结点而言，只有2号到4号结点和4号到2号结点的最短路经过1号结点，而2号结点和4号结点之间的最短路又有2条。因而根据定义，1号结点的重要程度计算为1/2+1/2=1。由于图的对称性，其他三个结点的重要程度也都是1。

50%的数据中：n ≤10，m ≤45

100%的数据中：n ≤100，m ≤4 500，任意一条边的权值c是正整数，满足：1 ≤c ≤1 000。

所有数据中保证给出的无向图连通，且任意两个结点之间的最短路径数目不超过10^10。

---

　　分析：

　　前几天做的题，不过现在才写。

　　首先这个奇奇怪怪的公式先不管，这么小的数据，当然可以$Floyd$啊。然后把这个公式转化成中文：以某个点为中心，求经过这个点的两点之间的最短路条数除以这两点的最短路的总条数，求个和。那就是最短路计数啊！当然，$Floyd$是可以做最短路计数的，不过蒟蒻当时并不知道。因此我用的是$Dijkstra$，以每个点为起点做一次最短路并求最短路计数即可。然后就是套公式了。

　　Code：

//It is made by HolseLee on 22nd Sep 2018
#include<queue>
#include<cmath>
#include<cstdio>
#include<cstring>
#include<iostream>
#include<algorithm>
#define N 107
#define M 4507
#define inf 1e9+7
using namespace std;

typedef long long ll;
int n,m,head[N],cnte,f[N][N];
ll s[N][N],p[N],dis[N],d[N][N];
double ans[N];
struct Edge {
    int to,val,nxt;
    Edge() {}
    Edge(const int &_x,const int &_y,const int &_z): to(_x),val(_y),nxt(_z) {}
}e[M<<];
struct Node {
    int x,d;
    Node() {}
    Node(const int &_x,const int &_y): x(_x),d(_y) {}
    bool operator < (const Node a) const {
        return d>a.d;
    }
};
priority_queue<Node> t;

inline int read()
{
    char ch=getchar(); int num=; bool flag=false;
    while( ch<'' || ch>'' ) {
        if( ch=='-' ) flag=true; ch=getchar();
    }
    while( ch>='' && ch<='' ) {
        num=num*+ch-''; ch=getchar();
    }
    return flag ? -num : num;
}

inline void add(int x,int y,int z)
{
    e[++cnte]=Edge(y,z,head[x]);
    head[x]=cnte;
}

inline void dij(int sta)
{
    for(int i=; i<=n; ++i)dis[i]=inf, p[i]=;
    while(!t.empty())t.pop();
    dis[sta]=, p[sta]=; t.push(Node(sta,));
    Node now; int x,y;
    while( !t.empty() ) {
        now=t.top(); t.pop();
        x=now.x;
        if( dis[x]<now.d ) continue;
        for(int i=head[x]; i; i=e[i].nxt) {
            y=e[i].to;
            if( dis[y]==dis[x]+e[i].val ) {
                p[y]+=p[x];continue;
            }
            if( dis[y]>dis[x]+e[i].val ){
                dis[y]=dis[x]+e[i].val;
                p[y]=p[x]; t.push(Node(y,dis[y]));
            }
        }
    }
}

int main()
{
    n=read(); m=read();
    int x,y,z;
    for(int i=; i<=m; ++i) {
        x=read(), y=read(), z=read();
        if( !f[x][y] || f[x][y]>z )
            f[x][y]=f[y][x]=z;
    }
    for(int i=; i<n; ++i)
    for(int j=i+; j<=n; ++j) {
        if( !f[i][j] ) continue;
        add(i,j,f[i][j]), add(j,i,f[j][i]);
    }
    for(int i=; i<=n; ++i) {
        dij(i);
        for(int j=; j<=n; ++j) {
            s[i][j]=p[j]; d[i][j]=dis[j];
        }
    }
    for(int i=; i<=n; ++i)
    for(int j=; j<=n; ++j)
    for(int k=; k<=n; ++k)
    if( j!=i && k!=i && j!=k ) {
        if( d[j][i]+d[i][k]!=d[j][k] )continue;
        if( !s[j][k] )continue;
        ans[i]+=(1.0*s[j][i]*s[i][k])/s[j][k];
    }
    for(int i=; i<=n; ++i)
    printf("%0.3lf\n",ans[i]);
    return ;
}